Question Number 3204 by Filup last updated on 07/Dec/15
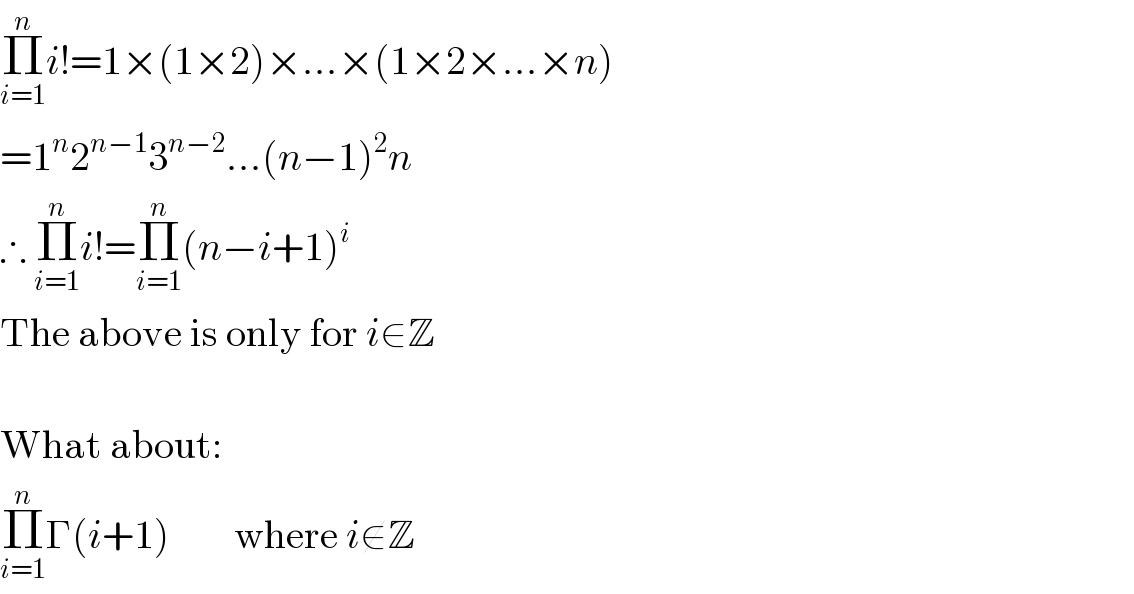
$$\underset{{i}=\mathrm{1}} {\overset{{n}} {\prod}}{i}!=\mathrm{1}×\left(\mathrm{1}×\mathrm{2}\right)×…×\left(\mathrm{1}×\mathrm{2}×…×{n}\right) \\ $$$$=\mathrm{1}^{{n}} \mathrm{2}^{{n}−\mathrm{1}} \mathrm{3}^{{n}−\mathrm{2}} …\left({n}−\mathrm{1}\right)^{\mathrm{2}} {n} \\ $$$$\therefore\:\underset{{i}=\mathrm{1}} {\overset{{n}} {\prod}}{i}!=\underset{{i}=\mathrm{1}} {\overset{{n}} {\prod}}\left({n}−{i}+\mathrm{1}\right)^{{i}} \\ $$$$\mathrm{The}\:\mathrm{above}\:\mathrm{is}\:\mathrm{only}\:\mathrm{for}\:{i}\in\mathbb{Z} \\ $$$$ \\ $$$$\mathrm{What}\:\mathrm{about}: \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{n}} {\prod}}\Gamma\left({i}+\mathrm{1}\right)\:\:\:\:\:\:\:\:\mathrm{where}\:{i}\notin\mathbb{Z} \\ $$
Commented by prakash jain last updated on 07/Dec/15

$$\mathrm{In}\:\mathrm{the}\:\mathrm{product}\:\mathrm{you}\:\mathrm{are}\:\mathrm{starting}\:\mathrm{with}\:{i}=\mathrm{1}\:\mathrm{and} \\ $$$$\mathrm{going}\:\mathrm{up}\:\mathrm{to}\:{n}.\:\mathrm{Generally}\:\mathrm{it}\:\mathrm{is}\:\mathrm{increment}\:\mathrm{by} \\ $$$$\mathrm{1}\:\mathrm{so}\:{i}\in\mathbb{Z}. \\ $$
