Menu Close

I-dx-x-x-2-1-3-

Tinku Tara 0 Comments
Pin




Question Number 132693 by liberty last updated on 15/Feb/21
I=∫ (dx/(x(x^2 +1)^3 ))
$$\mathrm{I}=\int\:\frac{{dx}}{{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\: \\ $$
Answered by EDWIN88 last updated on 15/Feb/21
Ostrogradsky again ∫ (dx/(x(x^2 +1)^3 )) = ((ax^3 +bx^2 +cx+d)/((x^2 +1)^2 ))+∫ ((ex^2 +fx+g)/(x(x^2 +1))) dx after solving for coefficient a=0 ,b=(1/2), c=0 , d=(3/4),e=0 ,f=0 and g=1 ∫ (dx/(x(x^2 +1)^3 )) = ((2x^2 +3)/(4(x^2 +1)^2 )) +∫ (1/(x(x^2 +1)))dx = ((2x^2 +3)/(4(x^2 +1)^2 ))+∫ ((1/x)−(x/(x^2 +1)))dx = ((2x^2 +3)/(4(x^2 +1)^2 ))+ln ∣x∣−(1/2)ln (x^2 +1) + C Ich mag dieses integral. scho^ ner ostrogradsky
$$\mathrm{Ostrogradsky}\:\mathrm{again} \\ $$$$\int\:\frac{{dx}}{{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\:=\:\frac{{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\int\:\frac{{ex}^{\mathrm{2}} +{fx}+{g}}{{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}\:{dx} \\ $$$${after}\:{solving}\:{for}\:{coefficient} \\ $$$${a}=\mathrm{0}\:,{b}=\frac{\mathrm{1}}{\mathrm{2}},\:{c}=\mathrm{0}\:,\:{d}=\frac{\mathrm{3}}{\mathrm{4}},\mathrm{e}=\mathrm{0}\:,\mathrm{f}=\mathrm{0}\:\mathrm{and}\:\mathrm{g}=\mathrm{1} \\ $$$$\int\:\frac{{dx}}{{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\:=\:\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}}{\mathrm{4}\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:+\int\:\frac{\mathrm{1}}{{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{dx} \\ $$$$\:\:\:\:\:\:\:=\:\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}}{\mathrm{4}\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\int\:\left(\frac{\mathrm{1}}{{x}}−\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\right){dx} \\ $$$$\:\:\:\:=\:\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}}{\mathrm{4}\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\mathrm{ln}\:\mid{x}\mid−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({x}^{\mathrm{2}} +\mathrm{1}\right)\:+\:{C}\: \\ $$$$\:\:\mathrm{Ich}\:\mathrm{mag}\:\mathrm{dieses}\:\mathrm{integral}.\:\mathrm{sch}\ddot {\mathrm{o}ner}\:\mathrm{ostrogradsky} \\ $$
Answered by mathmax by abdo last updated on 16/Feb/21
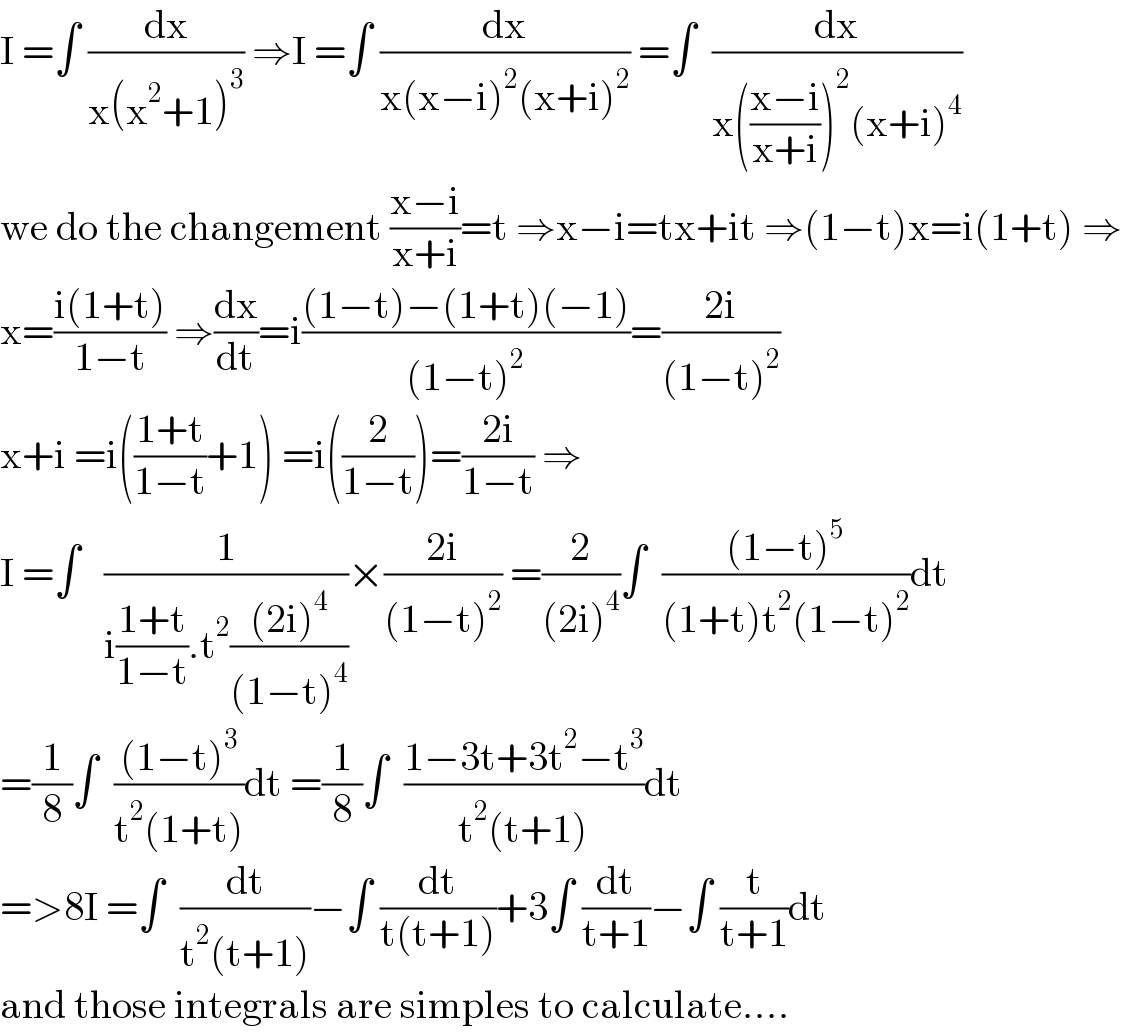
I =∫ (dx/(x(x^2 +1)^3 )) ⇒I =∫ (dx/(x(x−i)^2 (x+i)^2 )) =∫ (dx/(x(((x−i)/(x+i)))^2 (x+i)^4 )) we do the changement ((x−i)/(x+i))=t ⇒x−i=tx+it ⇒(1−t)x=i(1+t) ⇒ x=((i(1+t))/(1−t)) ⇒(dx/dt)=i(((1−t)−(1+t)(−1))/((1−t)^2 ))=((2i)/((1−t)^2 )) x+i =i(((1+t)/(1−t))+1) =i((2/(1−t)))=((2i)/(1−t)) ⇒ I =∫ (1/(i((1+t)/(1−t)).t^2 (((2i)^4 )/((1−t)^4 ))))×((2i)/((1−t)^2 )) =(2/((2i)^4 ))∫ (((1−t)^5 )/((1+t)t^2 (1−t)^2 ))dt =(1/8)∫ (((1−t)^3 )/(t^2 (1+t)))dt =(1/8)∫ ((1−3t+3t^2 −t^3 )/(t^2 (t+1)))dt =>8I =∫ (dt/(t^2 (t+1)))−∫ (dt/(t(t+1)))+3∫ (dt/(t+1))−∫ (t/(t+1))dt and those integrals are simples to calculate....
$$\mathrm{I}\:=\int\:\frac{\mathrm{dx}}{\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\:\Rightarrow\mathrm{I}\:=\int\:\frac{\mathrm{dx}}{\mathrm{x}\left(\mathrm{x}−\mathrm{i}\right)^{\mathrm{2}} \left(\mathrm{x}+\mathrm{i}\right)^{\mathrm{2}} }\:=\int\:\:\frac{\mathrm{dx}}{\mathrm{x}\left(\frac{\mathrm{x}−\mathrm{i}}{\mathrm{x}+\mathrm{i}}\right)^{\mathrm{2}} \left(\mathrm{x}+\mathrm{i}\right)^{\mathrm{4}} } \\ $$$$\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\frac{\mathrm{x}−\mathrm{i}}{\mathrm{x}+\mathrm{i}}=\mathrm{t}\:\Rightarrow\mathrm{x}−\mathrm{i}=\mathrm{tx}+\mathrm{it}\:\Rightarrow\left(\mathrm{1}−\mathrm{t}\right)\mathrm{x}=\mathrm{i}\left(\mathrm{1}+\mathrm{t}\right)\:\Rightarrow \\ $$$$\mathrm{x}=\frac{\mathrm{i}\left(\mathrm{1}+\mathrm{t}\right)}{\mathrm{1}−\mathrm{t}}\:\Rightarrow\frac{\mathrm{dx}}{\mathrm{dt}}=\mathrm{i}\frac{\left(\mathrm{1}−\mathrm{t}\right)−\left(\mathrm{1}+\mathrm{t}\right)\left(−\mathrm{1}\right)}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }=\frac{\mathrm{2i}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} } \\ $$$$\mathrm{x}+\mathrm{i}\:=\mathrm{i}\left(\frac{\mathrm{1}+\mathrm{t}}{\mathrm{1}−\mathrm{t}}+\mathrm{1}\right)\:=\mathrm{i}\left(\frac{\mathrm{2}}{\mathrm{1}−\mathrm{t}}\right)=\frac{\mathrm{2i}}{\mathrm{1}−\mathrm{t}}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\:\:\frac{\mathrm{1}}{\mathrm{i}\frac{\mathrm{1}+\mathrm{t}}{\mathrm{1}−\mathrm{t}}.\mathrm{t}^{\mathrm{2}} \frac{\left(\mathrm{2i}\right)^{\mathrm{4}} }{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{4}} }}×\frac{\mathrm{2i}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }\:=\frac{\mathrm{2}}{\left(\mathrm{2i}\right)^{\mathrm{4}} }\int\:\:\frac{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{5}} }{\left(\mathrm{1}+\mathrm{t}\right)\mathrm{t}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int\:\:\frac{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{3}} }{\mathrm{t}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{t}\right)}\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{8}}\int\:\:\frac{\mathrm{1}−\mathrm{3t}+\mathrm{3t}^{\mathrm{2}} −\mathrm{t}^{\mathrm{3}} }{\mathrm{t}^{\mathrm{2}} \left(\mathrm{t}+\mathrm{1}\right)}\mathrm{dt} \\ $$$$=>\mathrm{8I}\:=\int\:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \left(\mathrm{t}+\mathrm{1}\right)}−\int\:\frac{\mathrm{dt}}{\mathrm{t}\left(\mathrm{t}+\mathrm{1}\right)}+\mathrm{3}\int\:\frac{\mathrm{dt}}{\mathrm{t}+\mathrm{1}}−\int\:\frac{\mathrm{t}}{\mathrm{t}+\mathrm{1}}\mathrm{dt} \\ $$$$\mathrm{and}\:\mathrm{those}\:\mathrm{integrals}\:\mathrm{are}\:\mathrm{simples}\:\mathrm{to}\:\mathrm{calculate}…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *