Menu Close

I-have-2-buckets-Each-bucket-contains-green-and-blue-balls-The-first-bucket-contains-3-green-balls-and-7-blue-balls-Second-bucket-contains-7-green-balls-and-8-blue-balls-I-want-to-take-those-balls-

Tinku Tara 0 Comments
Pin




Question Number 9662 by Joel575 last updated on 23/Dec/16
I have 2 buckets. Each bucket contains green and blue balls The first bucket contains 3 green balls and 7 blue balls. Second bucket contains 7 green balls and 8 blue balls. I want to take those balls with coin toss. If head, I will take 1 ball from each bucket. But if tail, I will take 2 balls from each bucket. What is the propability if all the balls that have been taken have the same color? (sorry for my grammar)
$$\mathrm{I}\:\mathrm{have}\:\mathrm{2}\:\mathrm{buckets}.\:\mathrm{Each}\:\mathrm{bucket}\:\mathrm{contains}\:\mathrm{green}\:\mathrm{and}\:\mathrm{blue}\:\mathrm{balls} \\ $$$$\mathrm{The}\:\mathrm{first}\:\mathrm{bucket}\:\mathrm{contains}\:\mathrm{3}\:\mathrm{green}\:\mathrm{balls}\:\mathrm{and}\:\mathrm{7}\:\mathrm{blue}\:\mathrm{balls}. \\ $$$$\mathrm{Second}\:\mathrm{bucket}\:\mathrm{contains}\:\mathrm{7}\:\mathrm{green}\:\mathrm{balls}\:\mathrm{and}\:\mathrm{8}\:\mathrm{blue}\:\mathrm{balls}. \\ $$$$\mathrm{I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{take}\:\mathrm{those}\:\mathrm{balls}\:\mathrm{with}\:\mathrm{coin}\:\mathrm{toss}. \\ $$$$\mathrm{If}\:\mathrm{head},\:\mathrm{I}\:\mathrm{will}\:\mathrm{take}\:\mathrm{1}\:\mathrm{ball}\:\mathrm{from}\:\mathrm{each}\:\mathrm{bucket}. \\ $$$$\mathrm{But}\:\mathrm{if}\:\mathrm{tail},\:\mathrm{I}\:\mathrm{will}\:\mathrm{take}\:\mathrm{2}\:\mathrm{balls}\:\mathrm{from}\:\mathrm{each}\:\mathrm{bucket}. \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{propability}\:\mathrm{if}\:\mathrm{all}\:\mathrm{the}\:\mathrm{balls}\:\mathrm{that}\:\mathrm{have}\:\mathrm{been}\:\mathrm{taken} \\ $$$$\mathrm{have}\:\mathrm{the}\:\mathrm{same}\:\mathrm{color}? \\ $$$$\left({sorry}\:{for}\:{my}\:{grammar}\right) \\ $$
Answered by sandy_suhendra last updated on 23/Dec/16
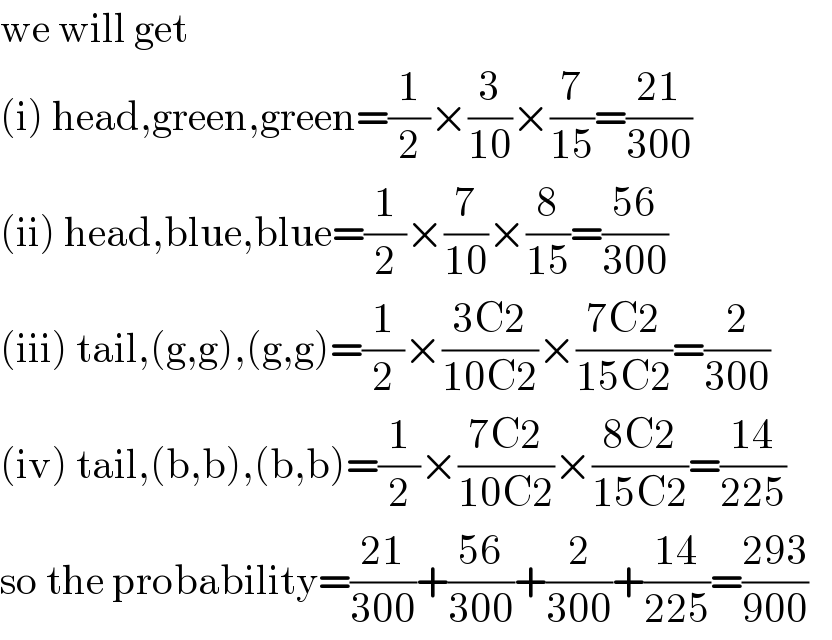
we will get (i) head,green,green=(1/2)×(3/(10))×(7/(15))=((21)/(300)) (ii) head,blue,blue=(1/2)×(7/(10))×(8/(15))=((56)/(300)) (iii) tail,(g,g),(g,g)=(1/2)×((3C2)/(10C2))×((7C2)/(15C2))=(2/(300)) (iv) tail,(b,b),(b,b)=(1/2)×((7C2)/(10C2))×((8C2)/(15C2))=((14)/(225)) so the probability=((21)/(300))+((56)/(300))+(2/(300))+((14)/(225))=((293)/(900))
$$\mathrm{we}\:\mathrm{will}\:\mathrm{get} \\ $$$$\left(\mathrm{i}\right)\:\mathrm{head},\mathrm{green},\mathrm{green}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{3}}{\mathrm{10}}×\frac{\mathrm{7}}{\mathrm{15}}=\frac{\mathrm{21}}{\mathrm{300}} \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{head},\mathrm{blue},\mathrm{blue}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{7}}{\mathrm{10}}×\frac{\mathrm{8}}{\mathrm{15}}=\frac{\mathrm{56}}{\mathrm{300}} \\ $$$$\left(\mathrm{iii}\right)\:\mathrm{tail},\left(\mathrm{g},\mathrm{g}\right),\left(\mathrm{g},\mathrm{g}\right)=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{3C2}}{\mathrm{10C2}}×\frac{\mathrm{7C2}}{\mathrm{15C2}}=\frac{\mathrm{2}}{\mathrm{300}} \\ $$$$\left(\mathrm{iv}\right)\:\mathrm{tail},\left(\mathrm{b},\mathrm{b}\right),\left(\mathrm{b},\mathrm{b}\right)=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{7C2}}{\mathrm{10C2}}×\frac{\mathrm{8C2}}{\mathrm{15C2}}=\frac{\mathrm{14}}{\mathrm{225}} \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{probability}=\frac{\mathrm{21}}{\mathrm{300}}+\frac{\mathrm{56}}{\mathrm{300}}+\frac{\mathrm{2}}{\mathrm{300}}+\frac{\mathrm{14}}{\mathrm{225}}=\frac{\mathrm{293}}{\mathrm{900}}\:\:\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *