Menu Close

I-have-4-collinear-points-A-a-0-B-b-0-C-c-0-and-D-d-0-where-a-b-c-d-gt-0-Find-a-point-E-x-y-such-that-the-following-expression-is-minimised-2-AE-BE-CE-DE-

Tinku Tara 0 Comments
Pin




Question Number 2672 by Yozzi last updated on 24/Nov/15
I have 4 collinear points A(a,0), B(b,0), C(c,0) and D(d,0) where ∀a,b,c,d>0. Find a point E(x,y) such that the following expression is minimised: 2(AE+BE+CE+DE).
$${I}\:{have}\:\mathrm{4}\:{collinear}\:{points}\:{A}\left({a},\mathrm{0}\right), \\ $$$${B}\left({b},\mathrm{0}\right),\:{C}\left({c},\mathrm{0}\right)\:{and}\:{D}\left({d},\mathrm{0}\right)\:{where}\: \\ $$$$\forall{a},{b},{c},{d}>\mathrm{0}.\:{Find}\:{a}\:{point}\:{E}\left({x},{y}\right)\:{such} \\ $$$${that}\:{the}\:{following}\:{expression}\:{is} \\ $$$${minimised}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\left({AE}+{BE}+{CE}+{DE}\right). \\ $$
Commented by Rasheed Soomro last updated on 24/Nov/15
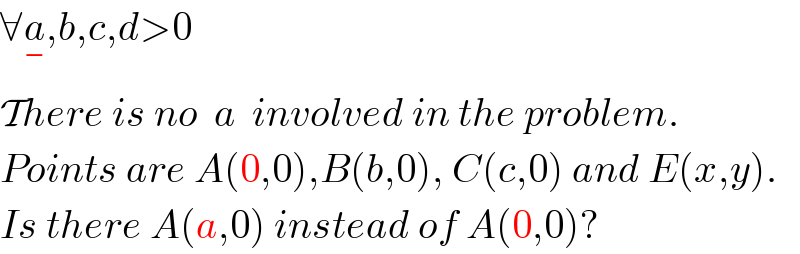
∀a_(−) ,b,c,d>0 There is no a involved in the problem. Points are A(0,0),B(b,0), C(c,0) and E(x,y). Is there A(a,0) instead of A(0,0)?
$$\forall\underset{−} {{a}},{b},{c},{d}>\mathrm{0} \\ $$$$\mathcal{T}{here}\:{is}\:{no}\:\:{a}\:\:{involved}\:{in}\:{the}\:{problem}. \\ $$$${Points}\:{are}\:{A}\left(\mathrm{0},\mathrm{0}\right),{B}\left({b},\mathrm{0}\right),\:{C}\left({c},\mathrm{0}\right)\:{and}\:{E}\left({x},{y}\right). \\ $$$${Is}\:{there}\:{A}\left({a},\mathrm{0}\right)\:{instead}\:{of}\:{A}\left(\mathrm{0},\mathrm{0}\right)? \\ $$
Commented by Yozzi last updated on 24/Nov/15
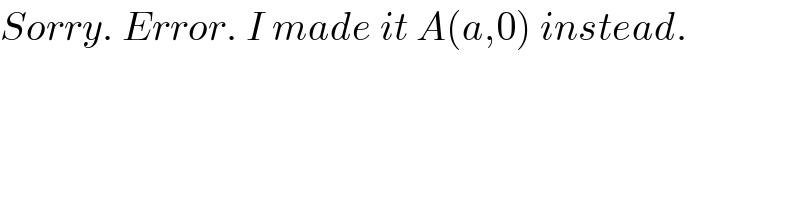
Sorry. Error. I made it A(a,0) instead.
$${Sorry}.\:{Error}.\:{I}\:{made}\:{it}\:{A}\left({a},\mathrm{0}\right)\:{instead}. \\ $$
Answered by prakash jain last updated on 24/Nov/15
assume a<b<c<d Consider 3 points BCE. BE+CE≥BC. BE+CE=BC when E is on the same line as BC and in between them. b≤x≤d Similarly for points ADE. a≤x≤d I am assuming A′s coordinate is (a,0). If a<b<c<d Then coordinated for point E are (x,0) where b≤x≤c (assuming a<b<c<d).
$$\mathrm{assume}\:{a}<{b}<{c}<{d} \\ $$$$\mathrm{Consider}\:\mathrm{3}\:\mathrm{points}\:\mathrm{BCE}. \\ $$$$\mathrm{BE}+\mathrm{CE}\geqslant\mathrm{BC}. \\ $$$$\mathrm{BE}+\mathrm{CE}=\mathrm{BC}\:\mathrm{when}\:\mathrm{E}\:\mathrm{is}\:\mathrm{on}\:\mathrm{the}\:\mathrm{same}\:\mathrm{line}\:\mathrm{as}\:\mathrm{BC} \\ $$$$\mathrm{and}\:\mathrm{in}\:\mathrm{between}\:\mathrm{them}. \\ $$$${b}\leqslant{x}\leqslant{d} \\ $$$$\mathrm{Similarly}\:\mathrm{for}\:\mathrm{points}\:\mathrm{ADE}.\:{a}\leqslant{x}\leqslant{d} \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{assuming}\:\mathrm{A}'{s}\:\mathrm{coordinate}\:\mathrm{is}\:\left({a},\mathrm{0}\right). \\ $$$$\mathrm{If}\:{a}<{b}<{c}<{d} \\ $$$$\mathrm{Then}\:\mathrm{coordinated}\:\mathrm{for}\:\mathrm{point}\:\mathrm{E}\:\mathrm{are} \\ $$$$\left({x},\mathrm{0}\right)\:\mathrm{where}\:{b}\leqslant{x}\leqslant{c}\:\left({assuming}\:{a}<{b}<{c}<{d}\right). \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *