Question Number 3894 by Filup last updated on 24/Dec/15

Commented by Filup last updated on 24/Dec/15
Commented by Filup last updated on 24/Dec/15
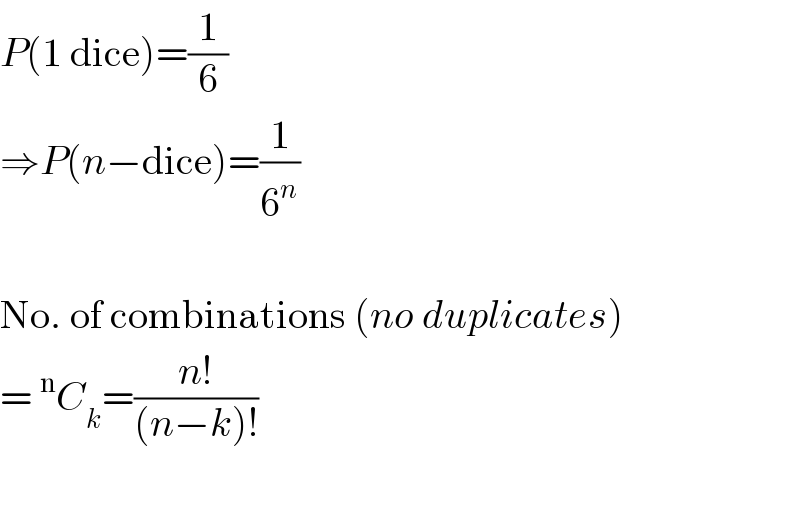
Commented by Yozzii last updated on 24/Dec/15
Commented by Filup last updated on 24/Dec/15
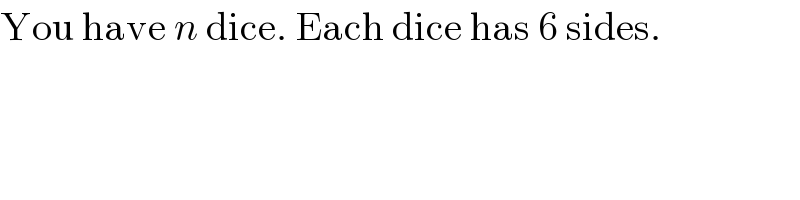
Commented by Yozzii last updated on 24/Dec/15
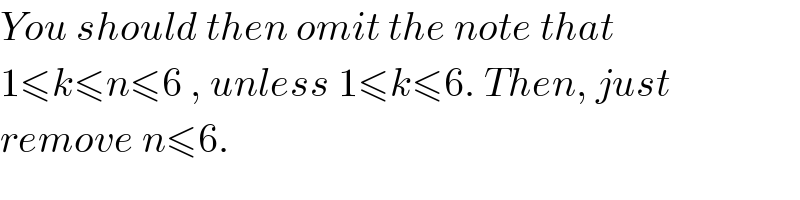
Answered by prakash jain last updated on 24/Dec/15
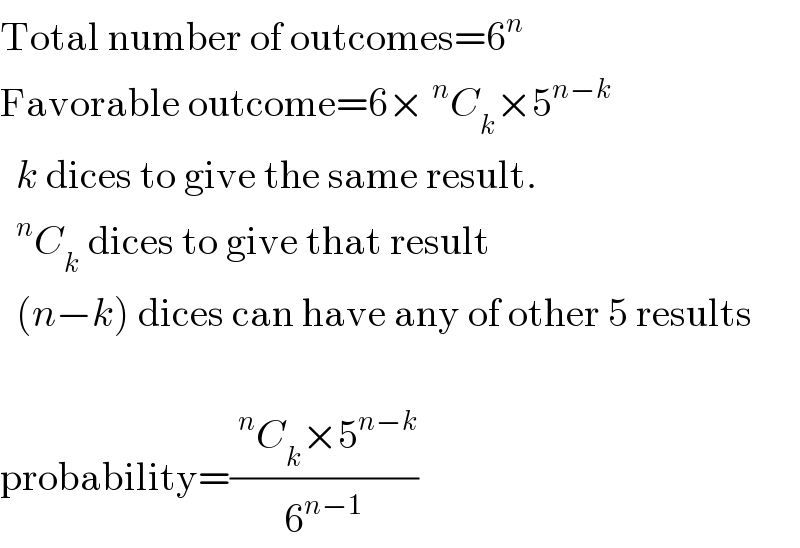
Commented by Yozzii last updated on 25/Dec/15
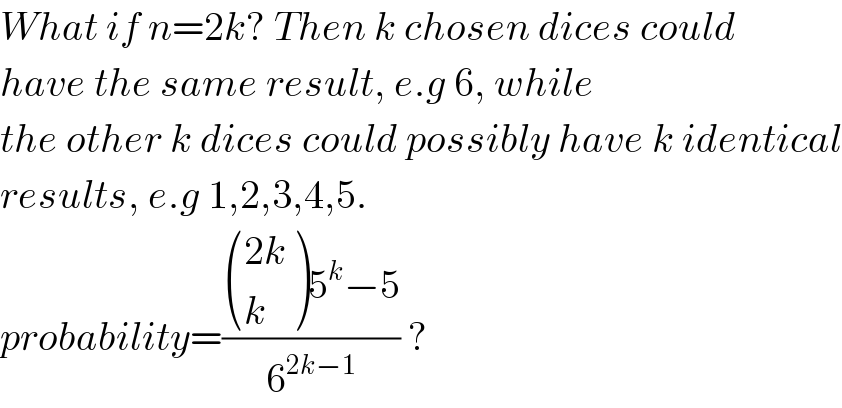
Commented by prakash jain last updated on 25/Dec/15
Commented by Yozzii last updated on 25/Dec/15
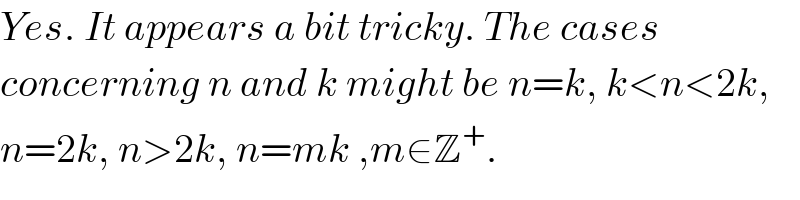
Commented by prakash jain last updated on 25/Dec/15

