Question Number 138209 by 676597498 last updated on 11/Apr/21
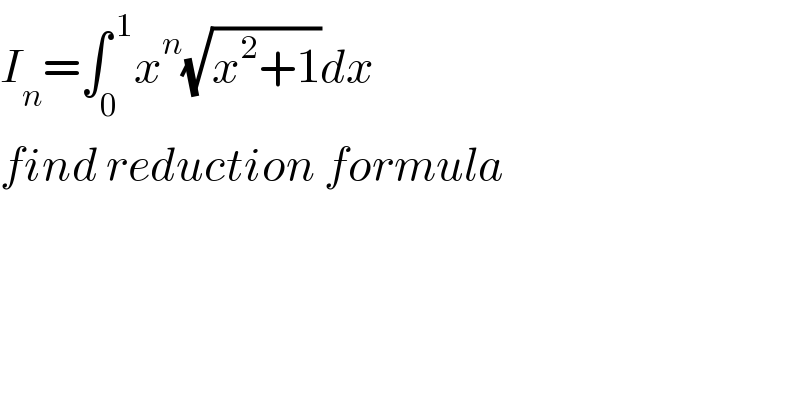
$${I}_{{n}} =\int_{\mathrm{0}} ^{\:\mathrm{1}} {x}^{{n}} \sqrt{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$${find}\:{reduction}\:{formula} \\ $$
Commented by Dwaipayan Shikari last updated on 11/Apr/21
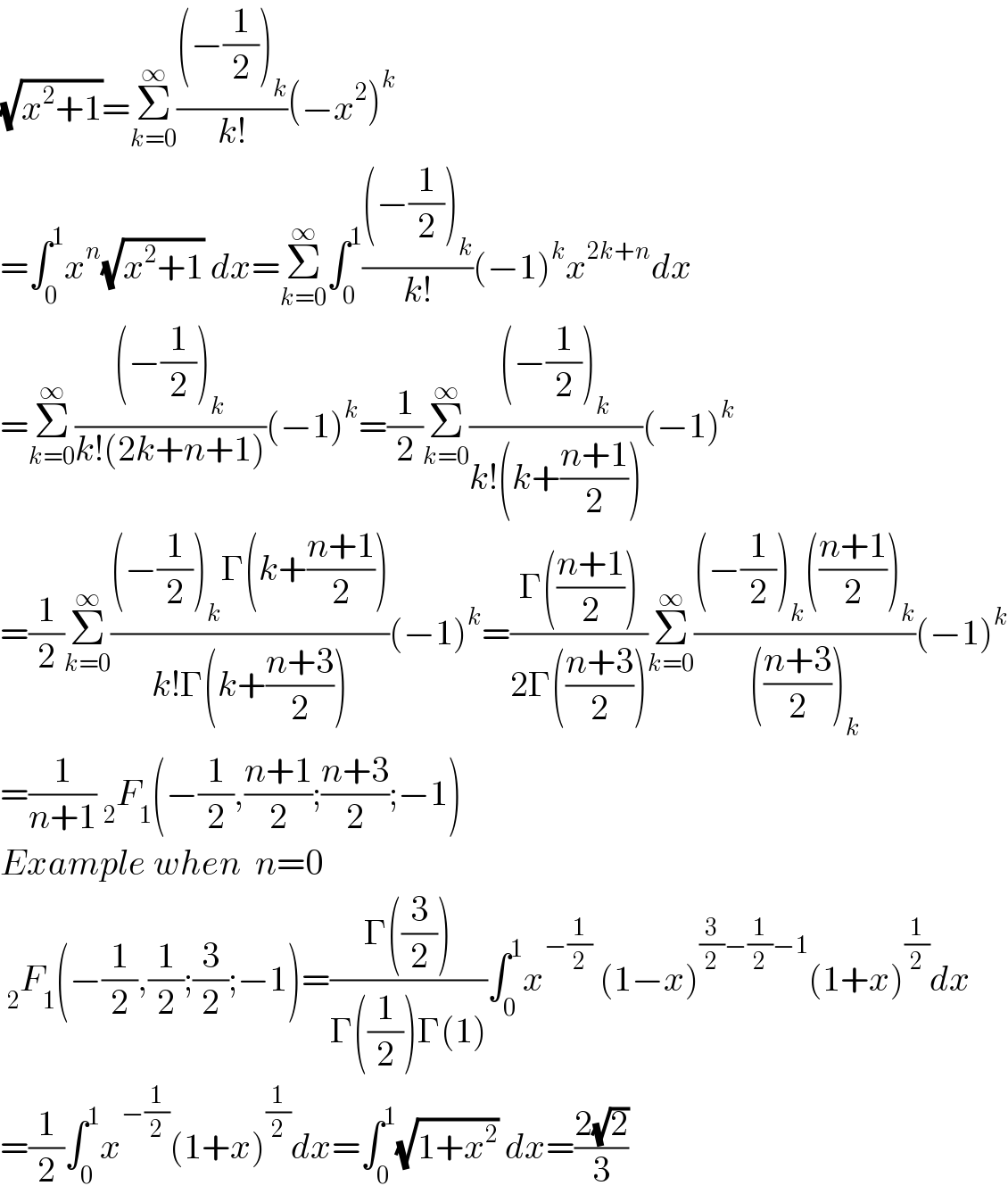
$$\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)_{{k}} }{{k}!}\left(−{x}^{\mathrm{2}} \right)^{{k}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:{dx}=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)_{{k}} }{{k}!}\left(−\mathrm{1}\right)^{{k}} {x}^{\mathrm{2}{k}+{n}} {dx} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)_{{k}} }{{k}!\left(\mathrm{2}{k}+{n}+\mathrm{1}\right)}\left(−\mathrm{1}\right)^{{k}} =\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)_{{k}} }{{k}!\left({k}+\frac{{n}+\mathrm{1}}{\mathrm{2}}\right)}\left(−\mathrm{1}\right)^{{k}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)_{{k}} \Gamma\left({k}+\frac{{n}+\mathrm{1}}{\mathrm{2}}\right)}{{k}!\Gamma\left({k}+\frac{{n}+\mathrm{3}}{\mathrm{2}}\right)}\left(−\mathrm{1}\right)^{{k}} =\frac{\Gamma\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}\Gamma\left(\frac{{n}+\mathrm{3}}{\mathrm{2}}\right)}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)_{{k}} \left(\frac{{n}+\mathrm{1}}{\mathrm{2}}\right)_{{k}} }{\left(\frac{{n}+\mathrm{3}}{\mathrm{2}}\right)_{{k}} }\left(−\mathrm{1}\right)^{{k}} \\ $$$$=\frac{\mathrm{1}}{{n}+\mathrm{1}}\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(−\frac{\mathrm{1}}{\mathrm{2}},\frac{{n}+\mathrm{1}}{\mathrm{2}};\frac{{n}+\mathrm{3}}{\mathrm{2}};−\mathrm{1}\right) \\ $$$${Example}\:{when}\:\:{n}=\mathrm{0} \\ $$$$\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(−\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}};\frac{\mathrm{3}}{\mathrm{2}};−\mathrm{1}\right)=\frac{\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\mathrm{1}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$
Answered by physicstutes last updated on 11/Apr/21
![I_n = ∫_0 ^1 x^n (√(x^2 +1)) dx I_n = ∫_0 ^1 x^(n−1) x(√(x^2 +1)) dx let u = x^(n−1) and dv = x(√(x^2 +1)) dx ⇒ du = (n−1)x^(n−2) dx and v = (1/2)((2/3))(x^2 +1)^(3/2) ∴ I_n = [(x^(n−1) /3)(x^2 +1)^(3/2) ]_0 ^1 −(((n−1))/3)∫_0 ^1 x^(n−2) (x^2 +1)(√(x^2 +1)) dx I_n = (2^(3/2) /3) −(((n−1))/3)[∫_0 ^1 x^n (√(x^2 +1)) dx + ∫_0 ^1 x^(n−2) (√(x^2 +1)) dx] I_n = ((2(√2))/3)−(((n−1))/3)I_n −(((n−1))/3)I_(n−2) ⇒ I_n (((n+2)/3)) = ((2(√2))/3)−(((n−1))/3)I_(n−2) hence I_n = ((2(√2)−(n−1)I_(n−2) )/((n+2))), n ≥ 2](https://www.tinkutara.com/question/Q138234.png)
$${I}_{{n}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:{dx} \\ $$$${I}_{{n}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}−\mathrm{1}} {x}\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:{dx} \\ $$$$\mathrm{let}\:{u}\:=\:{x}^{{n}−\mathrm{1}} \:\mathrm{and}\:{dv}\:=\:{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:{dx} \\ $$$$\Rightarrow\:{du}\:=\:\left({n}−\mathrm{1}\right){x}^{{n}−\mathrm{2}} \:{dx}\:\:\mathrm{and}\:{v}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} \\ $$$$\therefore\:\:{I}_{{n}} \:=\:\left[\frac{{x}^{{n}−\mathrm{1}} }{\mathrm{3}}\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right]_{\mathrm{0}} ^{\mathrm{1}} −\frac{\left({n}−\mathrm{1}\right)}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}−\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:{dx} \\ $$$$\:{I}_{{n}} \:=\:\frac{\mathrm{2}^{\mathrm{3}/\mathrm{2}} }{\mathrm{3}}\:−\frac{\left({n}−\mathrm{1}\right)}{\mathrm{3}}\left[\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:{dx}\:+\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}−\mathrm{2}} \sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:{dx}\right] \\ $$$$\:{I}_{{n}} \:=\:\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}−\frac{\left({n}−\mathrm{1}\right)}{\mathrm{3}}{I}_{{n}} −\frac{\left({n}−\mathrm{1}\right)}{\mathrm{3}}{I}_{{n}−\mathrm{2}} \\ $$$$\Rightarrow\:{I}_{{n}} \left(\frac{{n}+\mathrm{2}}{\mathrm{3}}\right)\:=\:\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}−\frac{\left({n}−\mathrm{1}\right)}{\mathrm{3}}{I}_{{n}−\mathrm{2}} \\ $$$$\mathrm{hence}\:{I}_{{n}} \:=\:\frac{\mathrm{2}\sqrt{\mathrm{2}}−\left({n}−\mathrm{1}\right){I}_{{n}−\mathrm{2}} }{\left({n}+\mathrm{2}\right)},\:{n}\:\geqslant\:\mathrm{2} \\ $$
Answered by mathmax by abdo last updated on 12/Apr/21
![I_n =∫_0 ^1 x^n (√(1+x^2 ))dx changement x=sht give I_n =∫_0 ^(argsh(1)) sh^n t ch(t)ch(t)dt =∫_0 ^(ln(1+(√2))) sh^n t cht(cht) dt (u^′ =cht sh^n t and v=cht) =[(1/(n+1))sh^(n+1) t cht]_0 ^(ln(1+(√2))) −(1/(n+1))∫_0 ^(ln(1+(√2))) sh^(n+2) t dt =(1/(n+1)){ ((e^t +e^(−t) )/2)(((e^t −e^(−t) )/2))^(n+1) ]_0 ^(ln(1+(√2))) −J_n =(1/(n+1)2^(n+2) )){(1+(√2)+(1+(√2))^(−1) )(1+(√2)−(1+(√2))^(−1) )^(n+1) } −J_n (n+1)J_n =∫_0 ^(ln(1+(√2))) (((e^t −e^(−t) )/2))^(n+2) dt =(1/2^(n+2) )∫_0 ^(ln(1+(√2))) Σ_(k=0) ^(n+2) C_k ^(n+2) (e^t )^k (−e^(−t) )^(n+2−k) dt =(1/2^(n+2) )Σ_(k=0) ^(n+2) C_(n+2) ^k (−1)^(n+2−k) ∫_0 ^(ln(1+(√2))) e^(kt) .e^(−(n+2−k)t) dt =(1/2^(n+2) )Σ_(k=0) ^(n+2) C_(n+2) ^k (−1)^(n−k) ∫_0 ^(ln(1+(√2))) e^((2k−n−2)t) dt and ∫_0 ^(ln(1+(√2))) e^((2k−n−2)t) =[(1/(2k−n−2))e^((2k−n−2)t) ]_0 ^(ln(1+(√2))) =(1/(2k−n−2))((1+(√2))^(2k−n−2) −1) ⇒ J_n =(1/((n+1)2^(n+2) ))Σ_(k=0) ^(n+2) (−1)^(n−k) C_(n+2) ^k .(1/(2k−n−2)){ (1+(√2))^(2k−n−2) −1} so the value of I_n is known...](https://www.tinkutara.com/question/Q138343.png)
$$\mathrm{I}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} \sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{x}=\mathrm{sht}\:\mathrm{give} \\ $$$$\mathrm{I}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{argsh}\left(\mathrm{1}\right)} \mathrm{sh}^{\mathrm{n}} \mathrm{t}\:\:\mathrm{ch}\left(\mathrm{t}\right)\mathrm{ch}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \mathrm{sh}^{\mathrm{n}} \mathrm{t}\:\mathrm{cht}\left(\mathrm{cht}\right)\:\:\mathrm{dt}\:\:\left(\mathrm{u}^{'} \:=\mathrm{cht}\:\mathrm{sh}^{\mathrm{n}} \mathrm{t}\:\:\mathrm{and}\:\mathrm{v}=\mathrm{cht}\right) \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\mathrm{sh}^{\mathrm{n}+\mathrm{1}} \mathrm{t}\:\mathrm{cht}\right]_{\mathrm{0}} ^{\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} −\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \mathrm{sh}^{\mathrm{n}+\mathrm{2}} \mathrm{t}\:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\left\{\:\:\frac{\mathrm{e}^{\mathrm{t}} +\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}\left(\frac{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}\right)^{\mathrm{n}+\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} −\mathrm{J}_{\mathrm{n}} \\ $$$$=\frac{\mathrm{1}}{\left.\mathrm{n}+\mathrm{1}\right)\mathrm{2}^{\mathrm{n}+\mathrm{2}} }\left\{\left(\mathrm{1}+\sqrt{\mathrm{2}}+\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{−\mathrm{1}} \right)\left(\mathrm{1}+\sqrt{\mathrm{2}}−\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{−\mathrm{1}} \right)^{\mathrm{n}+\mathrm{1}} \right\}\:−\mathrm{J}_{\mathrm{n}} \\ $$$$\left(\mathrm{n}+\mathrm{1}\right)\mathrm{J}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \left(\frac{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}\right)^{\mathrm{n}+\mathrm{2}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}+\mathrm{2}} }\int_{\mathrm{0}} ^{\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}+\mathrm{2}} \:\mathrm{C}_{\mathrm{k}} ^{\mathrm{n}+\mathrm{2}} \:\left(\mathrm{e}^{\mathrm{t}} \right)^{\mathrm{k}} \left(−\mathrm{e}^{−\mathrm{t}} \right)^{\mathrm{n}+\mathrm{2}−\mathrm{k}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}+\mathrm{2}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}+\mathrm{2}} \:\mathrm{C}_{\mathrm{n}+\mathrm{2}} ^{\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{2}−\mathrm{k}} \:\int_{\mathrm{0}} ^{\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:\mathrm{e}^{\mathrm{kt}} \:\:.\mathrm{e}^{−\left(\mathrm{n}+\mathrm{2}−\mathrm{k}\right)\mathrm{t}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}+\mathrm{2}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}+\mathrm{2}} \:\mathrm{C}_{\mathrm{n}+\mathrm{2}} ^{\mathrm{k}} \:\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{k}} \:\int_{\mathrm{0}} ^{\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:\mathrm{e}^{\left(\mathrm{2k}−\mathrm{n}−\mathrm{2}\right)\mathrm{t}} \:\mathrm{dt} \\ $$$$\mathrm{and}\:\int_{\mathrm{0}} ^{\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:\mathrm{e}^{\left(\mathrm{2k}−\mathrm{n}−\mathrm{2}\right)\mathrm{t}} \:=\left[\frac{\mathrm{1}}{\mathrm{2k}−\mathrm{n}−\mathrm{2}}\mathrm{e}^{\left(\mathrm{2k}−\mathrm{n}−\mathrm{2}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2k}−\mathrm{n}−\mathrm{2}}\left(\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2k}−\mathrm{n}−\mathrm{2}} −\mathrm{1}\right)\:\Rightarrow \\ $$$$\mathrm{J}_{\mathrm{n}} =\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{2}^{\mathrm{n}+\mathrm{2}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}+\mathrm{2}} \:\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{k}} \:\mathrm{C}_{\mathrm{n}+\mathrm{2}} ^{\mathrm{k}} \:.\frac{\mathrm{1}}{\mathrm{2k}−\mathrm{n}−\mathrm{2}}\left\{\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2k}−\mathrm{n}−\mathrm{2}} −\mathrm{1}\right\} \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{I}_{\mathrm{n}} \:\mathrm{is}\:\mathrm{known}… \\ $$
