Question Number 6354 by sanusihammed last updated on 24/Jun/16
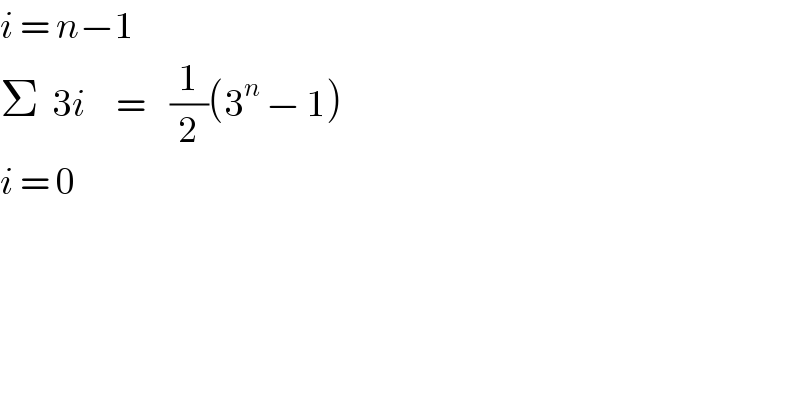
$${i}\:=\:{n}−\mathrm{1} \\ $$$$\Sigma\:\:\mathrm{3}{i}\:\:\:\:\:=\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}^{{n}} \:−\:\mathrm{1}\right) \\ $$$${i}\:=\:\mathrm{0} \\ $$
Commented by nburiburu last updated on 24/Jun/16
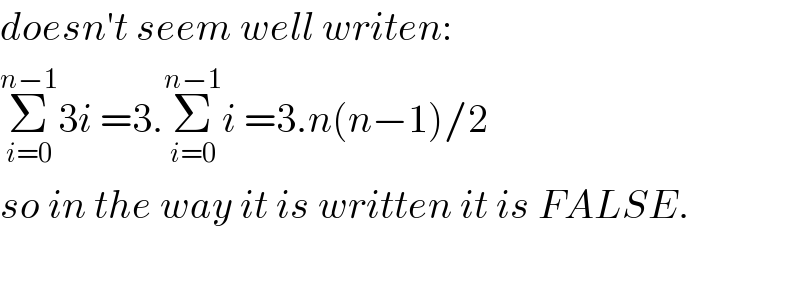
$${doesn}'{t}\:{seem}\:{well}\:{writen}: \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\mathrm{3}{i}\:=\mathrm{3}.\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{i}\:=\mathrm{3}.{n}\left({n}−\mathrm{1}\right)/\mathrm{2}\: \\ $$$${so}\:{in}\:{the}\:{way}\:{it}\:{is}\:{written}\:{it}\:{is}\:{FALSE}. \\ $$$$ \\ $$
Commented by prakash jain last updated on 24/Jun/16
![Σ_(i=0) ^(n−1) 3i≠(1/2)(3^n −1) n=3 LHS=0+3+6=9 RHS=(1/2)(3^3 −1)=13 The formula is correct if the question is Σ_(i=0) ^(n−1) 3^i proving for n=k+1 assuming result for n=k (1/2)(3^k −1)+=(1/2)[3^k −1+2∙3^k ] =(1/3)[3^k (2+1)−1]=(1/2)(3^(k+1) −1)](https://www.tinkutara.com/question/Q6363.png)
$$\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\mathrm{3}{i}\neq\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}^{{n}} −\mathrm{1}\right) \\ $$$${n}=\mathrm{3} \\ $$$$\mathrm{LHS}=\mathrm{0}+\mathrm{3}+\mathrm{6}=\mathrm{9} \\ $$$$\mathrm{RHS}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}^{\mathrm{3}} −\mathrm{1}\right)=\mathrm{13} \\ $$$$\mathrm{The}\:\mathrm{formula}\:\mathrm{is}\:\mathrm{correct}\:\mathrm{if}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is} \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\mathrm{3}^{{i}} \\ $$$${proving}\:{for}\:{n}={k}+\mathrm{1}\:{assuming}\:{result}\:{for}\:{n}={k} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}^{{k}} −\mathrm{1}\right)+=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{3}^{{k}} −\mathrm{1}+\mathrm{2}\centerdot\mathrm{3}^{{k}} \right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{3}^{{k}} \left(\mathrm{2}+\mathrm{1}\right)−\mathrm{1}\right]=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}^{{k}+\mathrm{1}} −\mathrm{1}\right) \\ $$
