Question Number 143961 by SOMEDAVONG last updated on 20/Jun/21
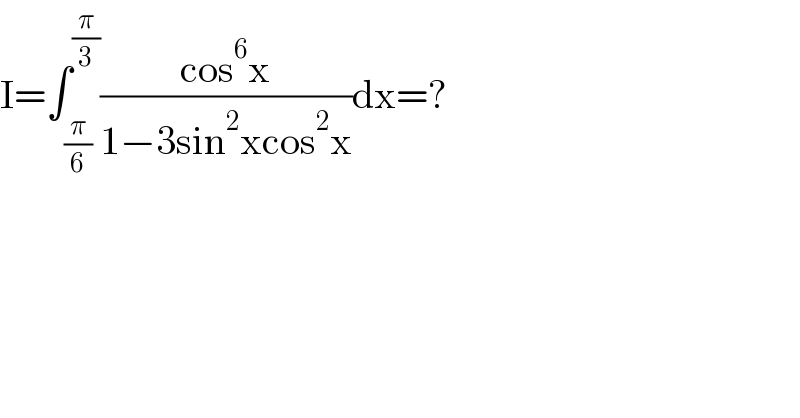
$$\mathrm{I}=\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \frac{\mathrm{cos}^{\mathrm{6}} \mathrm{x}}{\mathrm{1}−\mathrm{3sin}^{\mathrm{2}} \mathrm{xcos}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}=? \\ $$
Answered by Dwaipayan Shikari last updated on 20/Jun/21
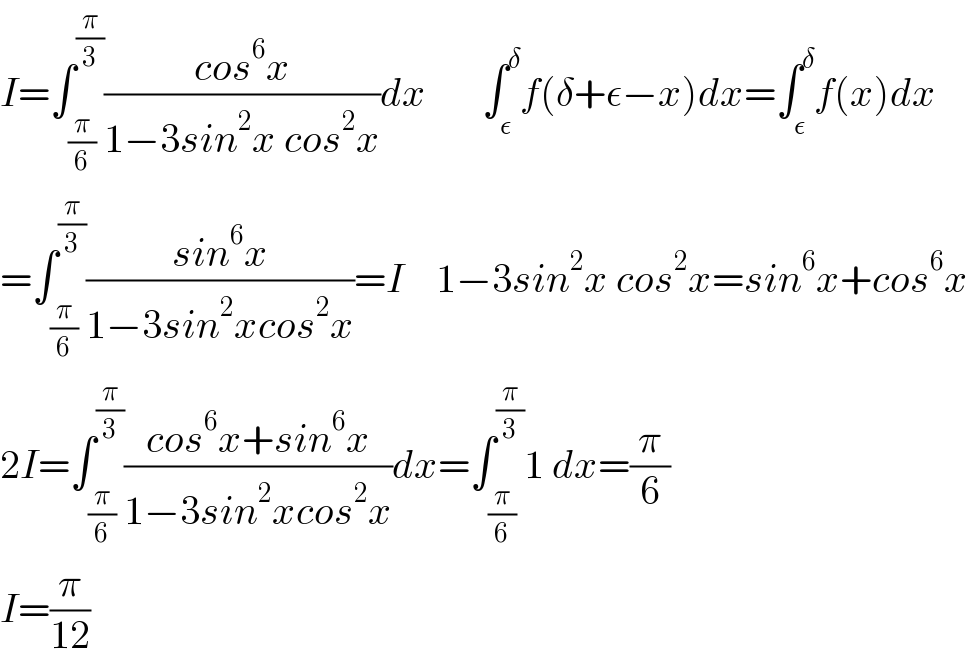
$${I}=\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \frac{{cos}^{\mathrm{6}} {x}}{\mathrm{1}−\mathrm{3}{sin}^{\mathrm{2}} {x}\:{cos}^{\mathrm{2}} {x}}{dx}\:\:\:\:\:\:\:\int_{\epsilon} ^{\delta} {f}\left(\delta+\epsilon−{x}\right){dx}=\int_{\epsilon} ^{\delta} {f}\left({x}\right){dx} \\ $$$$=\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \frac{{sin}^{\mathrm{6}} {x}}{\mathrm{1}−\mathrm{3}{sin}^{\mathrm{2}} {xcos}^{\mathrm{2}} {x}}={I}\:\:\:\:\mathrm{1}−\mathrm{3}{sin}^{\mathrm{2}} {x}\:{cos}^{\mathrm{2}} {x}={sin}^{\mathrm{6}} {x}+{cos}^{\mathrm{6}} {x} \\ $$$$\mathrm{2}{I}=\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \frac{{cos}^{\mathrm{6}} {x}+{sin}^{\mathrm{6}} {x}}{\mathrm{1}−\mathrm{3}{sin}^{\mathrm{2}} {xcos}^{\mathrm{2}} {x}}{dx}=\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \mathrm{1}\:{dx}=\frac{\pi}{\mathrm{6}} \\ $$$${I}=\frac{\pi}{\mathrm{12}} \\ $$
Commented by SOMEDAVONG last updated on 21/Jun/21

$$\mathrm{Thanks}\:\mathrm{sir}! \\ $$
