Menu Close

I-x-n-ax-b-dx-H-x-4-2x-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 134289 by bramlexs22 last updated on 02/Mar/21
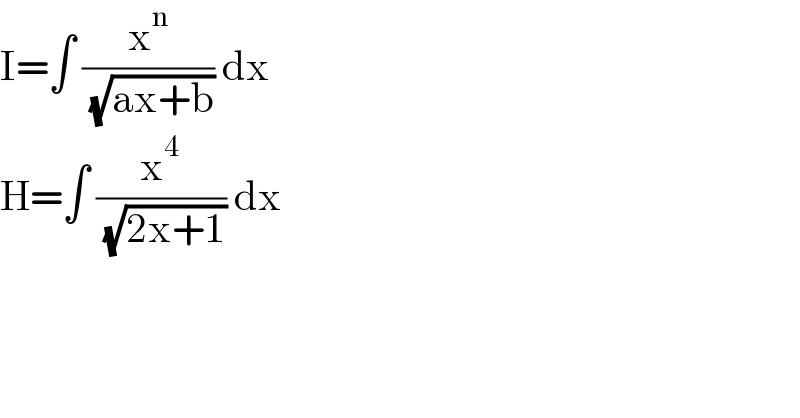
I=∫ (x^n /( (√(ax+b)))) dx H=∫ (x^4 /( (√(2x+1)))) dx
$$\mathrm{I}=\int\:\frac{\mathrm{x}^{\mathrm{n}} }{\:\sqrt{\mathrm{ax}+\mathrm{b}}}\:\mathrm{dx} \\ $$$$\mathrm{H}=\int\:\frac{\mathrm{x}^{\mathrm{4}} }{\:\sqrt{\mathrm{2x}+\mathrm{1}}}\:\mathrm{dx} \\ $$
Answered by EDWIN88 last updated on 02/Mar/21
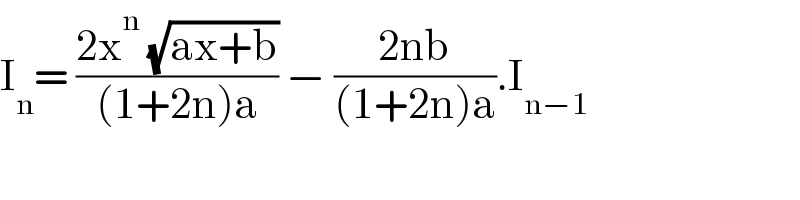
I_n = ((2x^n (√(ax+b)))/((1+2n)a)) − ((2nb)/((1+2n)a)).I_(n−1)
$$\mathrm{I}_{\mathrm{n}} =\:\frac{\mathrm{2x}^{\mathrm{n}} \:\sqrt{\mathrm{ax}+\mathrm{b}}}{\left(\mathrm{1}+\mathrm{2n}\right)\mathrm{a}}\:−\:\frac{\mathrm{2nb}}{\left(\mathrm{1}+\mathrm{2n}\right)\mathrm{a}}.\mathrm{I}_{\mathrm{n}−\mathrm{1}} \\ $$
Answered by EDWIN88 last updated on 02/Mar/21
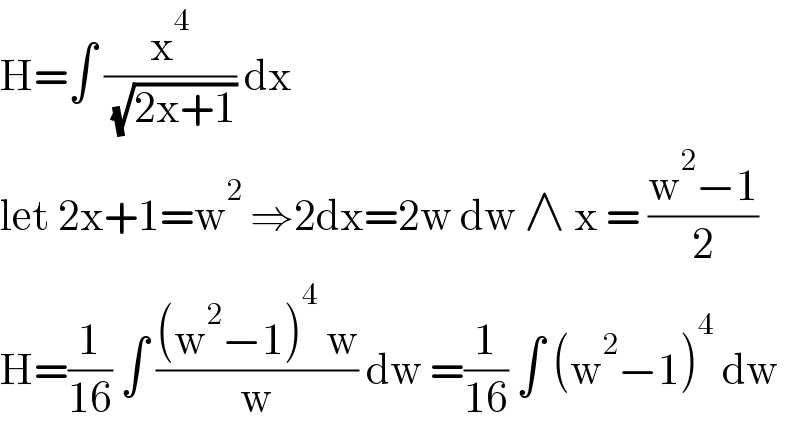
H=∫ (x^4 /( (√(2x+1)))) dx let 2x+1=w^2 ⇒2dx=2w dw ∧ x = ((w^2 −1)/2) H=(1/(16)) ∫ (((w^2 −1)^4 w)/w) dw =(1/(16)) ∫ (w^2 −1)^4 dw
$$\mathrm{H}=\int\:\frac{\mathrm{x}^{\mathrm{4}} }{\:\sqrt{\mathrm{2x}+\mathrm{1}}}\:\mathrm{dx}\: \\ $$$$\mathrm{let}\:\mathrm{2x}+\mathrm{1}=\mathrm{w}^{\mathrm{2}} \:\Rightarrow\mathrm{2dx}=\mathrm{2w}\:\mathrm{dw}\:\wedge\:\mathrm{x}\:=\:\frac{\mathrm{w}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{H}=\frac{\mathrm{1}}{\mathrm{16}}\:\int\:\frac{\left(\mathrm{w}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{4}} \:\mathrm{w}}{\mathrm{w}}\:\mathrm{dw}\:=\frac{\mathrm{1}}{\mathrm{16}}\:\int\:\left(\mathrm{w}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{4}} \:\mathrm{dw} \\ $$
Answered by mathmax by abdo last updated on 02/Mar/21
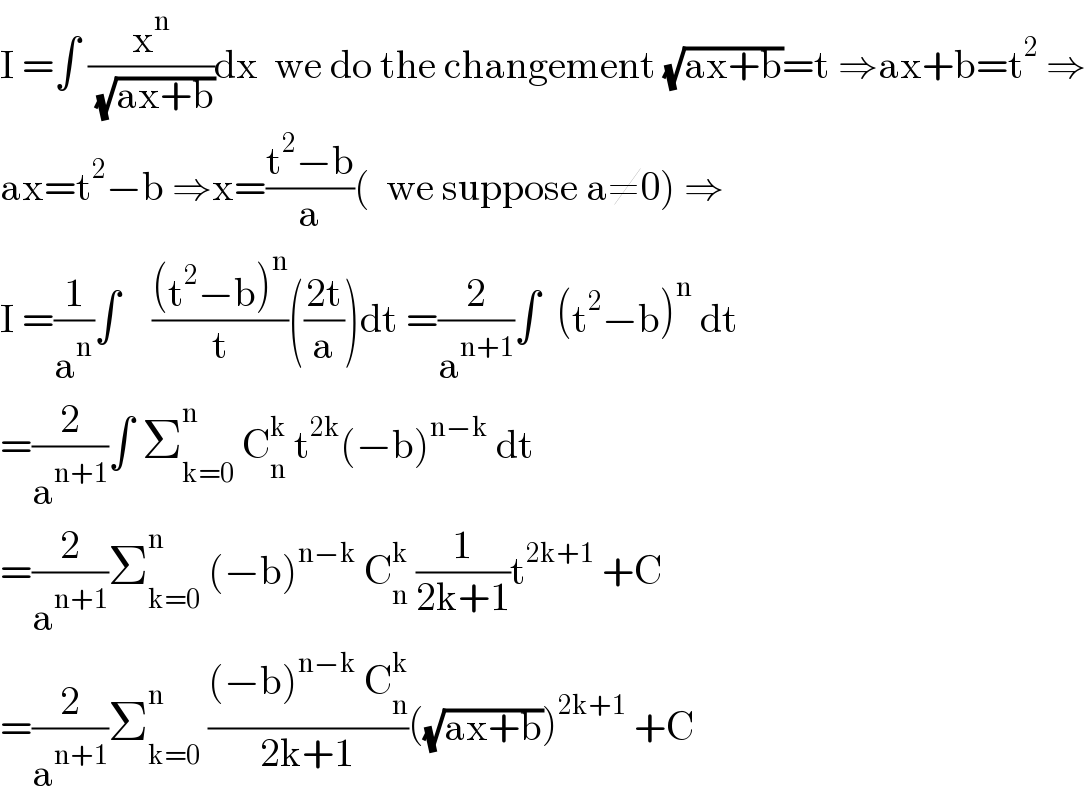
I =∫ (x^n /( (√(ax+b))))dx we do the changement (√(ax+b))=t ⇒ax+b=t^2 ⇒ ax=t^2 −b ⇒x=((t^2 −b)/a)( we suppose a≠0) ⇒ I =(1/a^n )∫ (((t^2 −b)^n )/t)(((2t)/a))dt =(2/a^(n+1) )∫ (t^2 −b)^n dt =(2/a^(n+1) )∫ Σ_(k=0) ^n C_n ^k t^(2k) (−b)^(n−k) dt =(2/a^(n+1) )Σ_(k=0) ^n (−b)^(n−k) C_n ^k (1/(2k+1))t^(2k+1) +C =(2/a^(n+1) )Σ_(k=0) ^n (((−b)^(n−k) C_n ^k )/(2k+1))((√(ax+b)))^(2k+1) +C
$$\mathrm{I}\:=\int\:\frac{\mathrm{x}^{\mathrm{n}} }{\:\sqrt{\mathrm{ax}+\mathrm{b}}}\mathrm{dx}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\sqrt{\mathrm{ax}+\mathrm{b}}=\mathrm{t}\:\Rightarrow\mathrm{ax}+\mathrm{b}=\mathrm{t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{ax}=\mathrm{t}^{\mathrm{2}} −\mathrm{b}\:\Rightarrow\mathrm{x}=\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{b}}{\mathrm{a}}\left(\:\:\mathrm{we}\:\mathrm{suppose}\:\mathrm{a}\neq\mathrm{0}\right)\:\Rightarrow \\ $$$$\mathrm{I}\:=\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{n}} }\int\:\:\:\:\frac{\left(\mathrm{t}^{\mathrm{2}} −\mathrm{b}\right)^{\mathrm{n}} }{\mathrm{t}}\left(\frac{\mathrm{2t}}{\mathrm{a}}\right)\mathrm{dt}\:=\frac{\mathrm{2}}{\mathrm{a}^{\mathrm{n}+\mathrm{1}} }\int\:\:\left(\mathrm{t}^{\mathrm{2}} −\mathrm{b}\right)^{\mathrm{n}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{2}}{\mathrm{a}^{\mathrm{n}+\mathrm{1}} }\int\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{t}^{\mathrm{2k}} \left(−\mathrm{b}\right)^{\mathrm{n}−\mathrm{k}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{2}}{\mathrm{a}^{\mathrm{n}+\mathrm{1}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\left(−\mathrm{b}\right)^{\mathrm{n}−\mathrm{k}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\frac{\mathrm{1}}{\mathrm{2k}+\mathrm{1}}\mathrm{t}^{\mathrm{2k}+\mathrm{1}} \:+\mathrm{C} \\ $$$$=\frac{\mathrm{2}}{\mathrm{a}^{\mathrm{n}+\mathrm{1}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{b}\right)^{\mathrm{n}−\mathrm{k}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} }{\mathrm{2k}+\mathrm{1}}\left(\sqrt{\mathrm{ax}+\mathrm{b}}\right)^{\mathrm{2k}+\mathrm{1}} \:+\mathrm{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *