Menu Close

If-0-lt-r-lt-1-is-S-convergent-in-the-following-S-a-2-ar-a-r-ar-2-a-2r-Determine-S-if-it-s-convergent-

Tinku Tara 0 Comments
Pin




Question Number 5744 by Rasheed Soomro last updated on 26/May/16
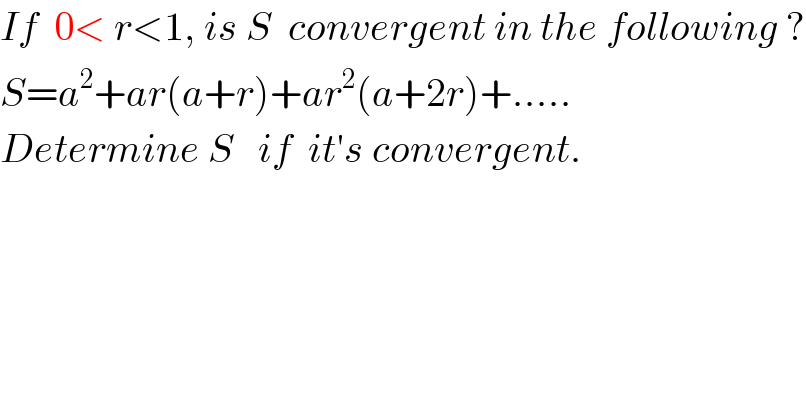
If 0< r<1, is S convergent in the following ? S=a^2 +ar(a+r)+ar^2 (a+2r)+..... Determine S if it′s convergent.
$${If}\:\:\mathrm{0}<\:{r}<\mathrm{1},\:{is}\:{S}\:\:{convergent}\:{in}\:{the}\:{following}\:? \\ $$$${S}={a}^{\mathrm{2}} +{ar}\left({a}+{r}\right)+{ar}^{\mathrm{2}} \left({a}+\mathrm{2}{r}\right)+….. \\ $$$${Determine}\:{S}\:\:\:{if}\:\:{it}'{s}\:{convergent}. \\ $$
Commented by FilupSmith last updated on 26/May/16
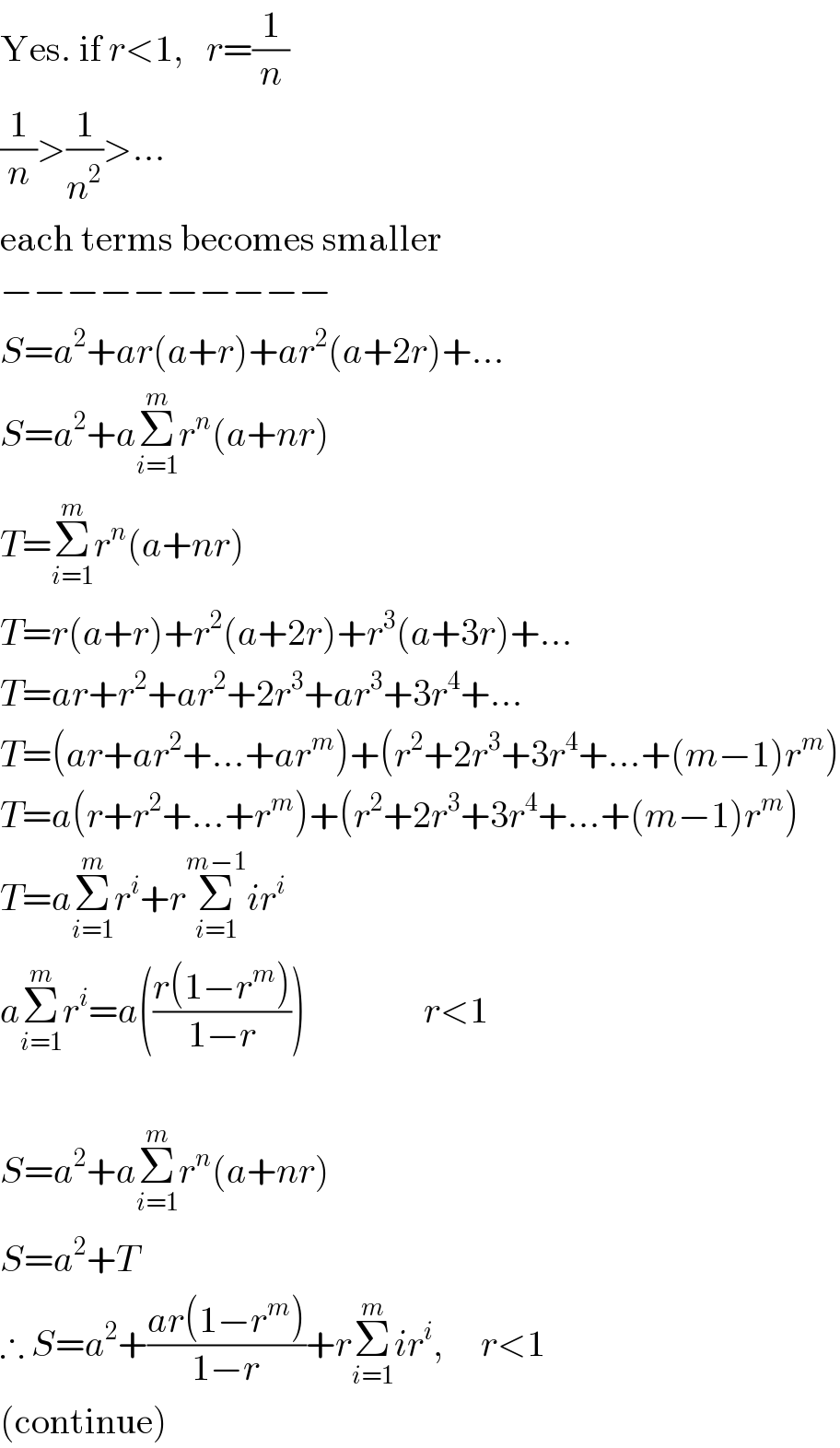
Yes. if r<1, r=(1/n) (1/n)>(1/n^2 )>... each terms becomes smaller −−−−−−−−−− S=a^2 +ar(a+r)+ar^2 (a+2r)+... S=a^2 +aΣ_(i=1) ^m r^n (a+nr) T=Σ_(i=1) ^m r^n (a+nr) T=r(a+r)+r^2 (a+2r)+r^3 (a+3r)+... T=ar+r^2 +ar^2 +2r^3 +ar^3 +3r^4 +... T=(ar+ar^2 +...+ar^m )+(r^2 +2r^3 +3r^4 +...+(m−1)r^m ) T=a(r+r^2 +...+r^m )+(r^2 +2r^3 +3r^4 +...+(m−1)r^m ) T=aΣ_(i=1) ^m r^i +rΣ_(i=1) ^(m−1) ir^i aΣ_(i=1) ^m r^i =a(((r(1−r^m ))/(1−r))) r<1 S=a^2 +aΣ_(i=1) ^m r^n (a+nr) S=a^2 +T ∴ S=a^2 +((ar(1−r^m ))/(1−r))+rΣ_(i=1) ^m ir^i , r<1 (continue)
$$\mathrm{Yes}.\:\mathrm{if}\:{r}<\mathrm{1},\:\:\:{r}=\frac{\mathrm{1}}{{n}} \\ $$$$\frac{\mathrm{1}}{{n}}>\frac{\mathrm{1}}{{n}^{\mathrm{2}} }>… \\ $$$$\mathrm{each}\:\mathrm{terms}\:\mathrm{becomes}\:\mathrm{smaller} \\ $$$$−−−−−−−−−− \\ $$$${S}={a}^{\mathrm{2}} +{ar}\left({a}+{r}\right)+{ar}^{\mathrm{2}} \left({a}+\mathrm{2}{r}\right)+… \\ $$$${S}={a}^{\mathrm{2}} +{a}\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}{r}^{{n}} \left({a}+{nr}\right) \\ $$$${T}=\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}{r}^{{n}} \left({a}+{nr}\right) \\ $$$${T}={r}\left({a}+{r}\right)+{r}^{\mathrm{2}} \left({a}+\mathrm{2}{r}\right)+{r}^{\mathrm{3}} \left({a}+\mathrm{3}{r}\right)+… \\ $$$${T}={ar}+{r}^{\mathrm{2}} +{ar}^{\mathrm{2}} +\mathrm{2}{r}^{\mathrm{3}} +{ar}^{\mathrm{3}} +\mathrm{3}{r}^{\mathrm{4}} +… \\ $$$${T}=\left({ar}+{ar}^{\mathrm{2}} +…+{ar}^{{m}} \right)+\left({r}^{\mathrm{2}} +\mathrm{2}{r}^{\mathrm{3}} +\mathrm{3}{r}^{\mathrm{4}} +…+\left({m}−\mathrm{1}\right){r}^{{m}} \right) \\ $$$${T}={a}\left({r}+{r}^{\mathrm{2}} +…+{r}^{{m}} \right)+\left({r}^{\mathrm{2}} +\mathrm{2}{r}^{\mathrm{3}} +\mathrm{3}{r}^{\mathrm{4}} +…+\left({m}−\mathrm{1}\right){r}^{{m}} \right) \\ $$$${T}={a}\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}{r}^{{i}} +{r}\underset{{i}=\mathrm{1}} {\overset{{m}−\mathrm{1}} {\sum}}{ir}^{{i}} \\ $$$${a}\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}{r}^{{i}} ={a}\left(\frac{{r}\left(\mathrm{1}−{r}^{{m}} \right)}{\mathrm{1}−{r}}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{r}<\mathrm{1} \\ $$$$ \\ $$$${S}={a}^{\mathrm{2}} +{a}\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}{r}^{{n}} \left({a}+{nr}\right) \\ $$$${S}={a}^{\mathrm{2}} +{T} \\ $$$$\therefore\:{S}={a}^{\mathrm{2}} +\frac{{ar}\left(\mathrm{1}−{r}^{{m}} \right)}{\mathrm{1}−{r}}+{r}\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}{ir}^{{i}} ,\:\:\:\:\:{r}<\mathrm{1} \\ $$$$\left(\mathrm{continue}\right) \\ $$
Commented by FilupSmith last updated on 26/May/16
I am sure my working is correct, but I am unsure how to continue
$$\mathrm{I}\:\mathrm{am}\:\mathrm{sure}\:\mathrm{my}\:\mathrm{working}\:\mathrm{is}\:\mathrm{correct},\:\mathrm{but} \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{unsure}\:\mathrm{how}\:\mathrm{to}\:\mathrm{continue} \\ $$
Commented by Rasheed Soomro last updated on 26/May/16
I didn′t consider about the solution.However I want to share with you how this question & Q#5742 came into my mind . I have created these questions as follows: Consider an A.P. and a G.P. having first term same (say a) and equal common difference and common ratio (say r). a, a+r, a+2r.... & a,ar,ar^2 .... Now consider a rectangle whose dimentions are corresponding terms of above sequence. All such rectangles form a sequence ...Sum of all rectangles....
$$\mathrm{I}\:\mathrm{didn}'\mathrm{t}\:\mathrm{consider}\:\mathrm{about}\:\mathrm{the}\:\mathrm{solution}.\mathrm{However}\:\mathrm{I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{share} \\ $$$$\mathrm{with}\:\mathrm{you}\:\mathrm{how}\:\mathrm{this}\:\mathrm{question}\:\&\:{Q}#\mathrm{5742}\:\mathrm{came}\:\mathrm{into}\:\mathrm{my}\:\mathrm{mind}\:. \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{have}\:\mathrm{created}\:\mathrm{these}\:\:\mathrm{questions}\:\:\mathrm{as}\:\mathrm{follows}: \\ $$$$\mathrm{Consider}\:\mathrm{an}\:\mathrm{A}.\mathrm{P}.\:\mathrm{and}\:\mathrm{a}\:\mathrm{G}.\mathrm{P}.\:\:\mathrm{having}\:\mathrm{first}\:\mathrm{term}\:\mathrm{same} \\ $$$$\left(\mathrm{say}\:{a}\right)\:\mathrm{and}\:\:\mathrm{equal}\:\mathrm{common}\:\mathrm{difference}\:\mathrm{and} \\ $$$$\mathrm{common}\:\mathrm{ratio}\:\left(\mathrm{say}\:{r}\right). \\ $$$${a},\:{a}+{r},\:{a}+\mathrm{2}{r}….\:\:\&\:\:\:\:{a},{ar},{ar}^{\mathrm{2}} …. \\ $$$$\mathrm{Now}\:\mathrm{consider}\:\mathrm{a}\:\mathrm{rectangle}\:\mathrm{whose}\:\mathrm{dimentions} \\ $$$$\mathrm{are}\:\mathrm{corresponding}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{above}\:\mathrm{sequence}. \\ $$$$\mathrm{All}\:\mathrm{such}\:\mathrm{rectangles}\:\mathrm{form}\:\mathrm{a}\:\mathrm{sequence}\:…\mathrm{Sum} \\ $$$$\mathrm{of}\:\mathrm{all}\:\mathrm{rectangles}…. \\ $$$$ \\ $$
Commented by FilupSmith last updated on 26/May/16
I see. I love doing these problems, also. Especially fractal−like shapes.
$$\mathrm{I}\:\mathrm{see}.\:\mathrm{I}\:\mathrm{love}\:\mathrm{doing}\:\mathrm{these}\:\mathrm{problems},\:\mathrm{also}. \\ $$$$\mathrm{Especially}\:\mathrm{fractal}−\mathrm{like}\:\mathrm{shapes}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *