Question Number 134475 by EDWIN88 last updated on 04/Mar/21

$$\mathrm{If}\:\mathrm{1}+\mathrm{cos}\:\mathrm{x}+\mathrm{cos}\:\mathrm{2x}+\mathrm{cos}\:\mathrm{3x}+\mathrm{cos}\:\mathrm{4x}+…+\infty\:=\:\mathrm{3} \\ $$$$\mathrm{for}\:\mathrm{0}<\mathrm{x}\leqslant\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{sin}\:\mathrm{x}+\mathrm{sin}\:\mathrm{2x}+\mathrm{sin}\:\mathrm{3x}+…+\infty \\ $$
Commented by Dwaipayan Shikari last updated on 04/Mar/21
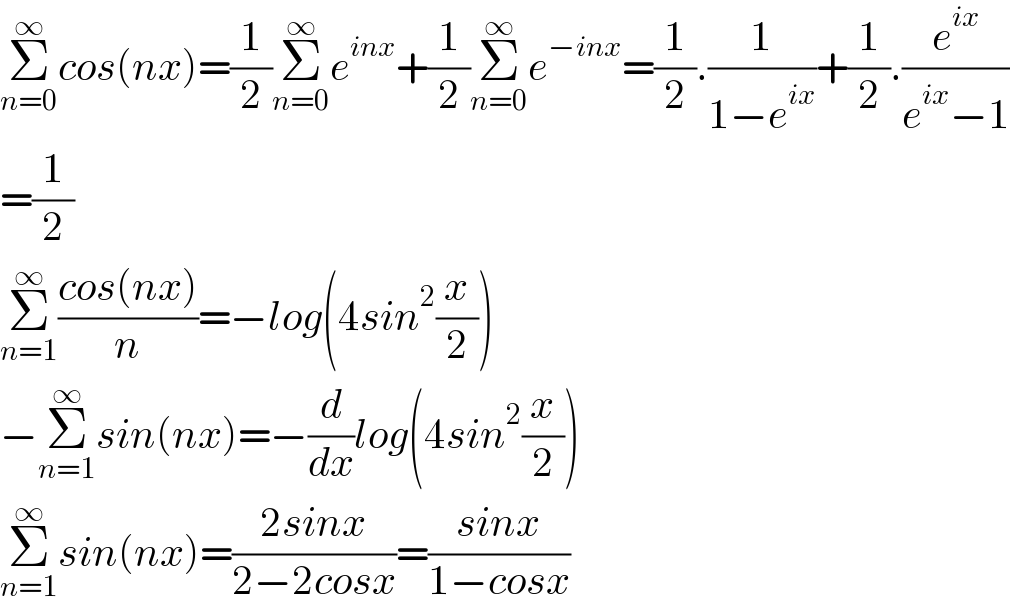
$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{cos}\left({nx}\right)=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{e}^{{inx}} +\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{e}^{−{inx}} =\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{1}−{e}^{{ix}} }+\frac{\mathrm{1}}{\mathrm{2}}.\frac{{e}^{{ix}} }{{e}^{{ix}} −\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\: \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{cos}\left({nx}\right)}{{n}}=−{log}\left(\mathrm{4}{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\right) \\ $$$$−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{sin}\left({nx}\right)=−\frac{{d}}{{dx}}{log}\left(\mathrm{4}{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{sin}\left({nx}\right)=\frac{\mathrm{2}{sinx}}{\mathrm{2}−\mathrm{2}{cosx}}=\frac{{sinx}}{\mathrm{1}−{cosx}} \\ $$
Commented by benjo_mathlover last updated on 04/Mar/21
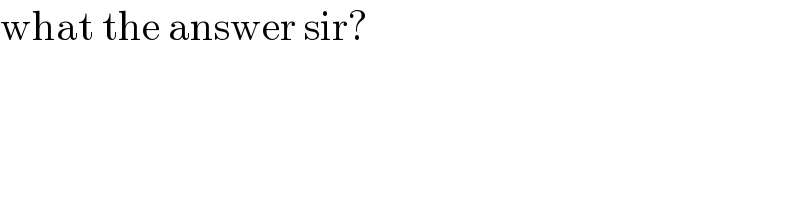
$$\mathrm{what}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{sir}? \\ $$
Commented by Dwaipayan Shikari last updated on 04/Mar/21
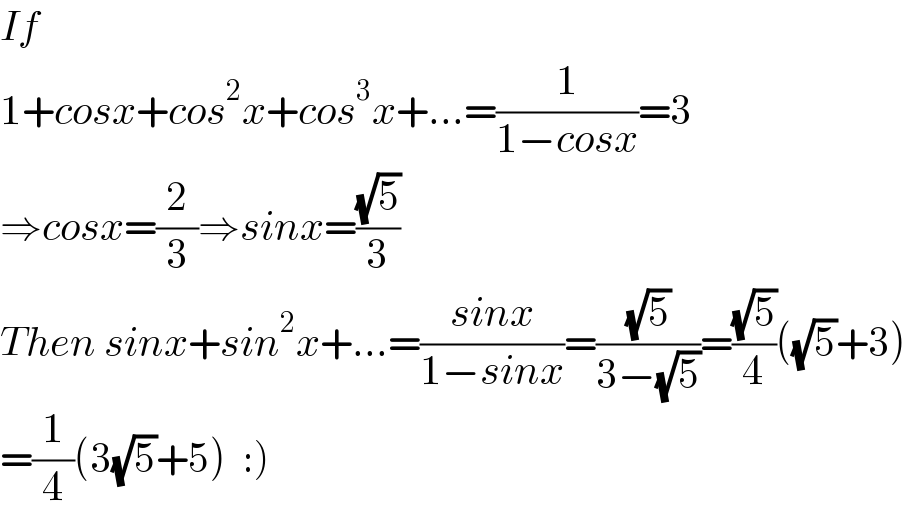
$${If}\:\: \\ $$$$\mathrm{1}+{cosx}+{cos}^{\mathrm{2}} {x}+{cos}^{\mathrm{3}} {x}+…=\frac{\mathrm{1}}{\mathrm{1}−{cosx}}=\mathrm{3} \\ $$$$\Rightarrow{cosx}=\frac{\mathrm{2}}{\mathrm{3}}\Rightarrow{sinx}=\frac{\sqrt{\mathrm{5}}}{\mathrm{3}} \\ $$$${Then}\:{sinx}+{sin}^{\mathrm{2}} {x}+…=\frac{{sinx}}{\mathrm{1}−{sinx}}=\frac{\sqrt{\mathrm{5}}}{\mathrm{3}−\sqrt{\mathrm{5}}}=\frac{\sqrt{\mathrm{5}}}{\mathrm{4}}\left(\sqrt{\mathrm{5}}+\mathrm{3}\right) \\ $$$$\left.=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{3}\sqrt{\mathrm{5}}+\mathrm{5}\right)\:\::\right) \\ $$
Commented by EDWIN88 last updated on 04/Mar/21
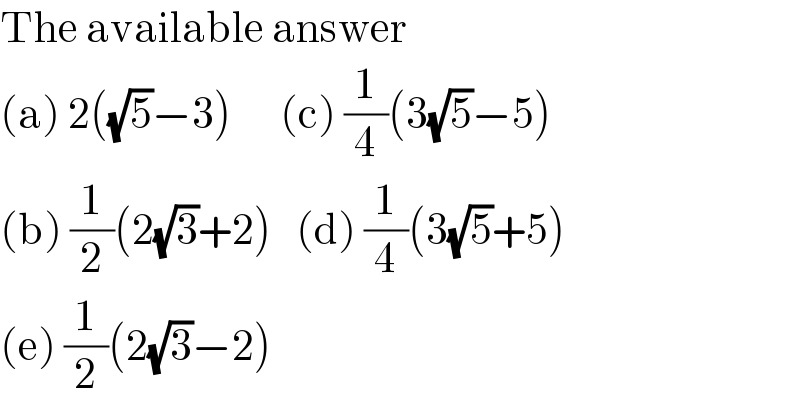
$$\mathrm{The}\:\mathrm{available}\:\mathrm{answer}\: \\ $$$$\left(\mathrm{a}\right)\:\mathrm{2}\left(\sqrt{\mathrm{5}}−\mathrm{3}\right)\:\:\:\:\:\:\left(\mathrm{c}\right)\:\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{3}\sqrt{\mathrm{5}}−\mathrm{5}\right) \\ $$$$\left(\mathrm{b}\right)\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{2}\right)\:\:\:\left(\mathrm{d}\right)\:\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{3}\sqrt{\mathrm{5}}+\mathrm{5}\right) \\ $$$$\left(\mathrm{e}\right)\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{2}\right) \\ $$
Commented by Dwaipayan Shikari last updated on 04/Mar/21
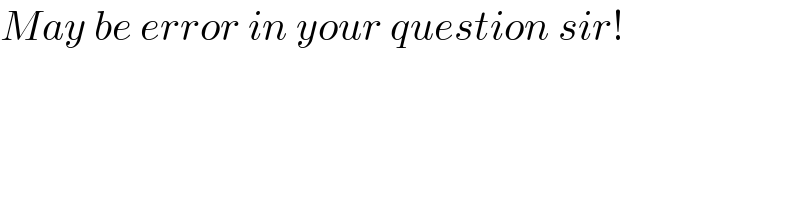
$${May}\:{be}\:{error}\:{in}\:{your}\:{question}\:{sir}! \\ $$
Commented by EDWIN88 last updated on 04/Mar/21

$$\mathrm{yes}\:\mathrm{sir}\:.\mathrm{i}\:\mathrm{think}\:\mathrm{it}\:\mathrm{wrong} \\ $$
