Question Number 8306 by lepan last updated on 07/Oct/16
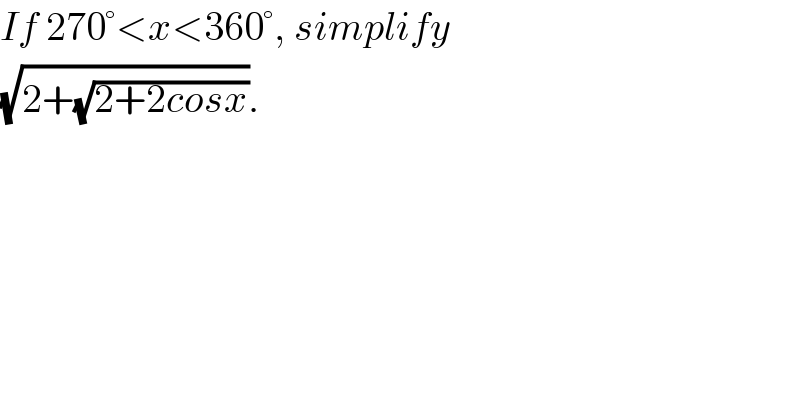
$${If}\:\mathrm{270}°<{x}<\mathrm{360}°,\:{simplify} \\ $$$$\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\mathrm{2}{cosx}}}. \\ $$
Commented by sou1618 last updated on 07/Oct/16
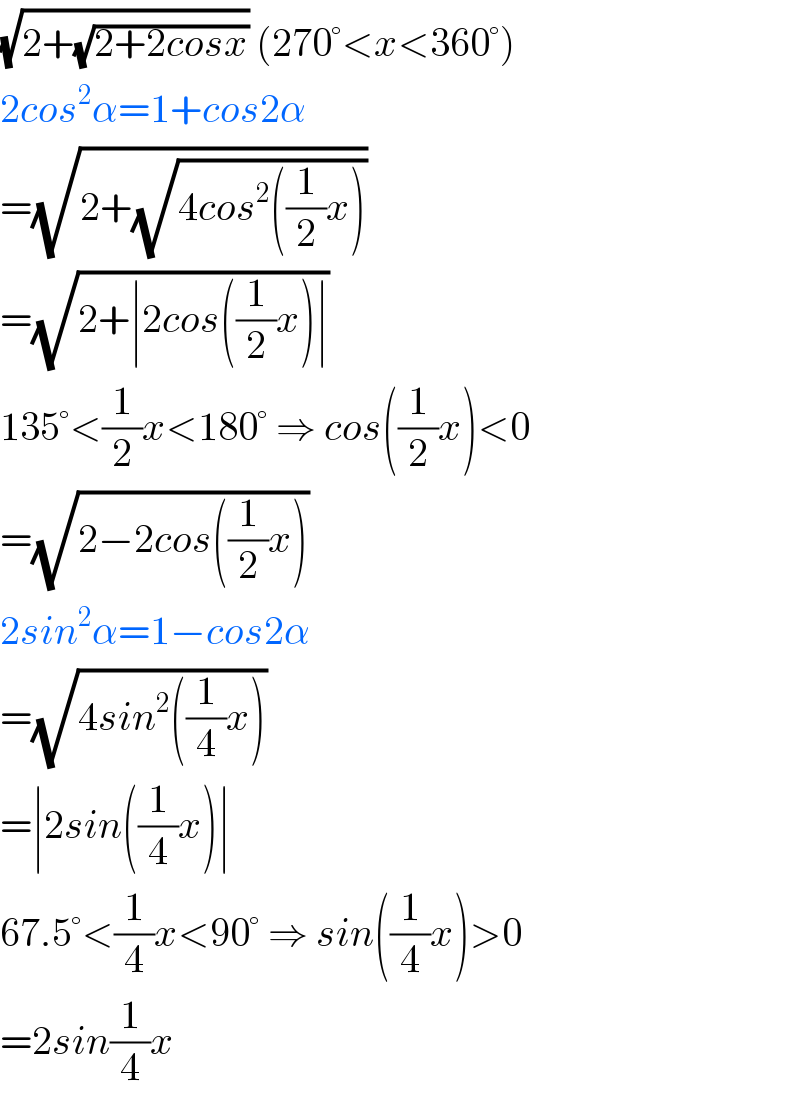
$$\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\mathrm{2}{cosx}}}\:\left(\mathrm{270}°<{x}<\mathrm{360}°\right) \\ $$$$\mathrm{2}{cos}^{\mathrm{2}} \alpha=\mathrm{1}+{cos}\mathrm{2}\alpha \\ $$$$=\sqrt{\mathrm{2}+\sqrt{\mathrm{4}{cos}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}{x}\right)}} \\ $$$$=\sqrt{\mathrm{2}+\mid\mathrm{2}{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}{x}\right)\mid} \\ $$$$\mathrm{135}°<\frac{\mathrm{1}}{\mathrm{2}}{x}<\mathrm{180}°\:\Rightarrow\:{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}{x}\right)<\mathrm{0} \\ $$$$=\sqrt{\mathrm{2}−\mathrm{2}{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}{x}\right)} \\ $$$$\mathrm{2}{sin}^{\mathrm{2}} \alpha=\mathrm{1}−{cos}\mathrm{2}\alpha \\ $$$$=\sqrt{\mathrm{4}{sin}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}{x}\right)} \\ $$$$=\mid\mathrm{2}{sin}\left(\frac{\mathrm{1}}{\mathrm{4}}{x}\right)\mid \\ $$$$\mathrm{67}.\mathrm{5}°<\frac{\mathrm{1}}{\mathrm{4}}{x}<\mathrm{90}°\:\Rightarrow\:{sin}\left(\frac{\mathrm{1}}{\mathrm{4}}{x}\right)>\mathrm{0} \\ $$$$=\mathrm{2}{sin}\frac{\mathrm{1}}{\mathrm{4}}{x} \\ $$
