Question Number 66354 by gunawan last updated on 13/Aug/19

$$\mathrm{If}\:\:\mathrm{2}{x}+{y}=\mathrm{8}\:\mathrm{and} \\ $$$$\left({x}+{y}\right)=\frac{\mathrm{3}}{\mathrm{2}}\mathrm{log}_{\mathrm{10}} \:\mathrm{2}.\mathrm{log}_{\mathrm{8}} \mathrm{36} \\ $$$$\mathrm{then}\:\mathrm{x}^{\mathrm{2}} +\mathrm{3y}=… \\ $$$$\mathrm{a}.\:\mathrm{28} \\ $$$$\mathrm{b}.\:\mathrm{22} \\ $$$$\mathrm{c}.\:\mathrm{20} \\ $$$$\mathrm{d}.\:\mathrm{16} \\ $$$$\mathrm{e}.\:\mathrm{12} \\ $$
Commented by kaivan.ahmadi last updated on 13/Aug/19
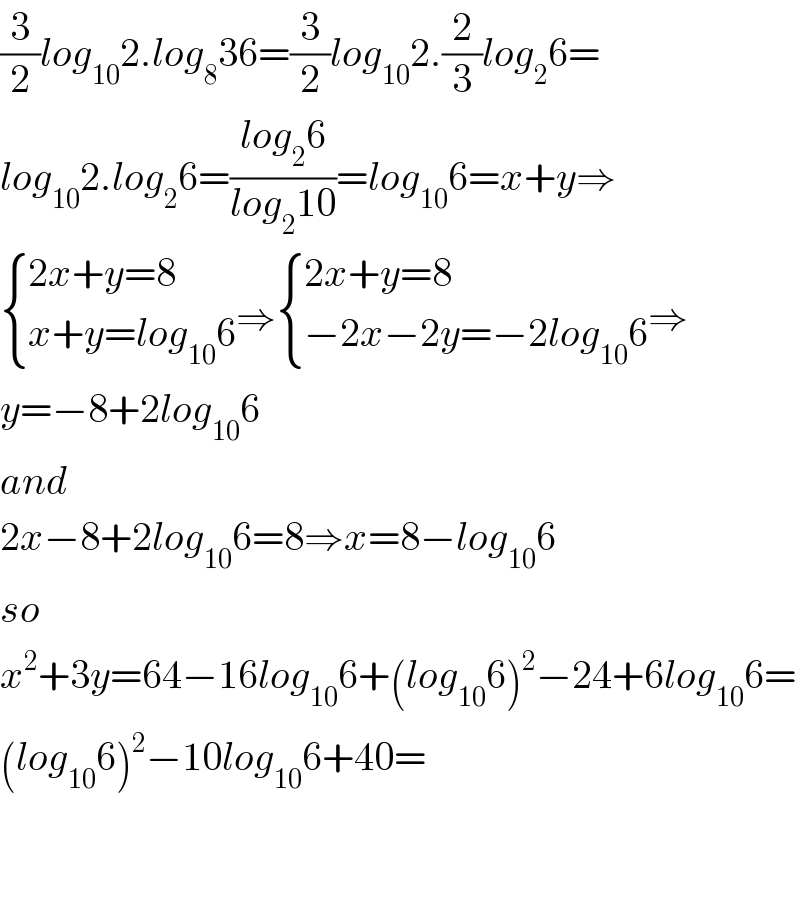
$$\frac{\mathrm{3}}{\mathrm{2}}{log}_{\mathrm{10}} \mathrm{2}.{log}_{\mathrm{8}} \mathrm{36}=\frac{\mathrm{3}}{\mathrm{2}}{log}_{\mathrm{10}} \mathrm{2}.\frac{\mathrm{2}}{\mathrm{3}}{log}_{\mathrm{2}} \mathrm{6}= \\ $$$${log}_{\mathrm{10}} \mathrm{2}.{log}_{\mathrm{2}} \mathrm{6}=\frac{{log}_{\mathrm{2}} \mathrm{6}}{{log}_{\mathrm{2}} \mathrm{10}}={log}_{\mathrm{10}} \mathrm{6}={x}+{y}\Rightarrow \\ $$$$\begin{cases}{\mathrm{2}{x}+{y}=\mathrm{8}}\\{{x}+{y}={log}_{\mathrm{10}} \mathrm{6}}\end{cases}\Rightarrow\begin{cases}{\mathrm{2}{x}+{y}=\mathrm{8}}\\{−\mathrm{2}{x}−\mathrm{2}{y}=−\mathrm{2}{log}_{\mathrm{10}} \mathrm{6}}\end{cases}\Rightarrow \\ $$$${y}=−\mathrm{8}+\mathrm{2}{log}_{\mathrm{10}} \mathrm{6} \\ $$$${and} \\ $$$$\mathrm{2}{x}−\mathrm{8}+\mathrm{2}{log}_{\mathrm{10}} \mathrm{6}=\mathrm{8}\Rightarrow{x}=\mathrm{8}−{log}_{\mathrm{10}} \mathrm{6} \\ $$$${so} \\ $$$${x}^{\mathrm{2}} +\mathrm{3}{y}=\mathrm{64}−\mathrm{16}{log}_{\mathrm{10}} \mathrm{6}+\left({log}_{\mathrm{10}} \mathrm{6}\right)^{\mathrm{2}} −\mathrm{24}+\mathrm{6}{log}_{\mathrm{10}} \mathrm{6}= \\ $$$$\left({log}_{\mathrm{10}} \mathrm{6}\right)^{\mathrm{2}} −\mathrm{10}{log}_{\mathrm{10}} \mathrm{6}+\mathrm{40}= \\ $$$$ \\ $$$$ \\ $$
