Question Number 138091 by liberty last updated on 10/Apr/21
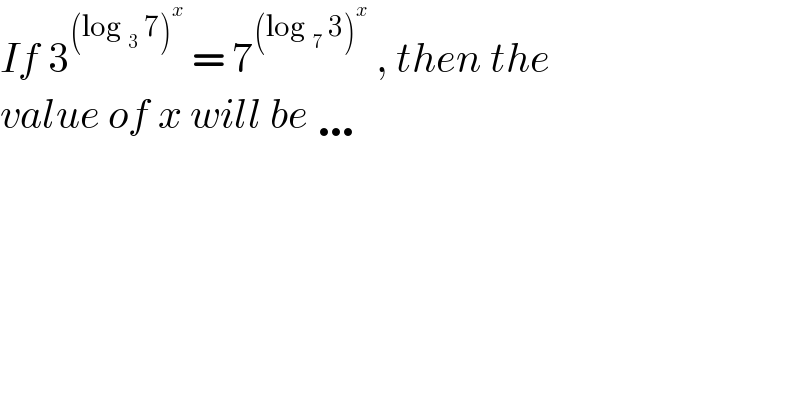
$${If}\:\mathrm{3}^{\left(\mathrm{log}\:_{\mathrm{3}} \:\mathrm{7}\right)^{{x}} } \:=\:\mathrm{7}^{\left(\mathrm{log}\:_{\mathrm{7}} \:\mathrm{3}\right)^{{x}} } \:,\:{then}\:{the} \\ $$$${value}\:{of}\:{x}\:{will}\:{be}\:\ldots\: \\ $$
Answered by mitica last updated on 10/Apr/21
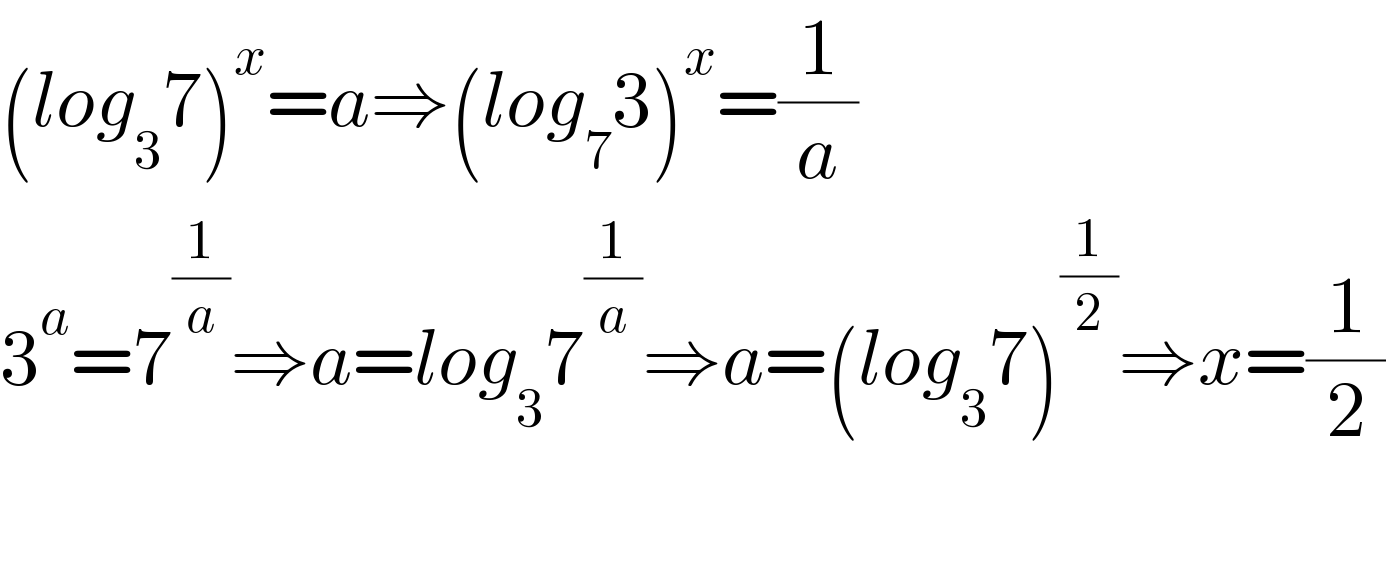
$$\left({log}_{\mathrm{3}} \mathrm{7}\right)^{{x}} ={a}\Rightarrow\left({log}_{\mathrm{7}} \mathrm{3}\right)^{{x}} =\frac{\mathrm{1}}{{a}} \\ $$$$\mathrm{3}^{{a}} =\mathrm{7}^{\frac{\mathrm{1}}{{a}}} \Rightarrow{a}={log}_{\mathrm{3}} \mathrm{7}^{\frac{\mathrm{1}}{{a}}} \Rightarrow{a}=\left({log}_{\mathrm{3}} \mathrm{7}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$
Answered by Ankushkumarparcha last updated on 10/Apr/21
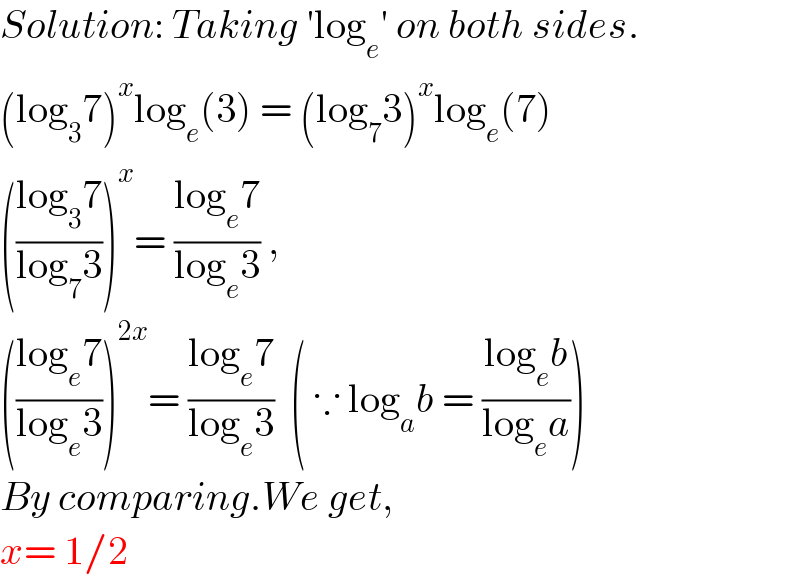
$${Solution}:\:{Taking}\:'\mathrm{log}_{{e}} '\:{on}\:{both}\:{sides}. \\ $$$$\left(\mathrm{log}_{\mathrm{3}} \mathrm{7}\right)^{{x}} \mathrm{log}_{{e}} \left(\mathrm{3}\right)\:=\:\left(\mathrm{log}_{\mathrm{7}} \mathrm{3}\right)^{{x}} \mathrm{log}_{{e}} \left(\mathrm{7}\right) \\ $$$$\left(\frac{\mathrm{log}_{\mathrm{3}} \mathrm{7}}{\mathrm{log}_{\mathrm{7}} \mathrm{3}}\right)^{{x}} =\:\frac{\mathrm{log}_{{e}} \mathrm{7}}{\mathrm{log}_{{e}} \mathrm{3}}\:, \\ $$$$\left(\frac{\mathrm{log}_{{e}} \mathrm{7}}{\mathrm{log}_{{e}} \mathrm{3}}\right)^{\mathrm{2}{x}} =\:\frac{\mathrm{log}_{{e}} \mathrm{7}}{\mathrm{log}_{{e}} \mathrm{3}}\:\:\left(\:\because\:\mathrm{log}_{{a}} {b}\:=\:\frac{\mathrm{log}_{{e}} {b}}{\mathrm{log}_{{e}} {a}}\right) \\ $$$${By}\:{comparing}.{We}\:{get}, \\ $$$${x}=\:\mathrm{1}/\mathrm{2} \\ $$
