Question Number 1304 by 314159 last updated on 20/Jul/15

$${If}\:\mathrm{3}^{{log}\:\mathrm{3}{x}} =\mathrm{4}^{{log}\:\mathrm{4}{x}} ,\:{find}\:{x}. \\ $$$$ \\ $$
Answered by Rasheed Soomro last updated on 20/Jul/15
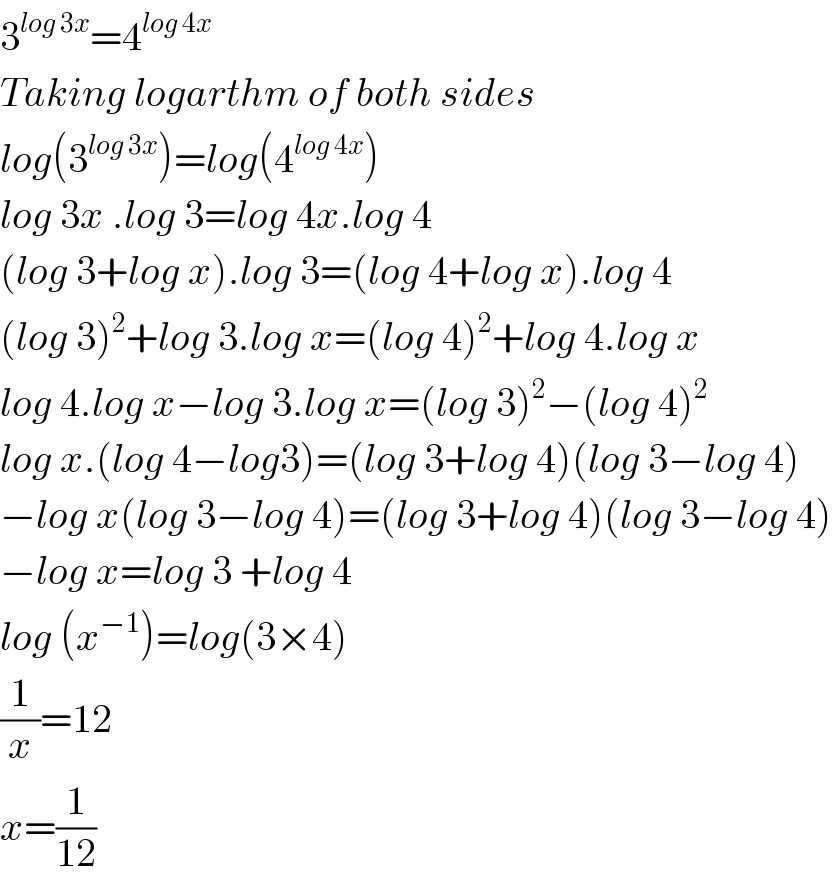
$$\mathrm{3}^{{log}\:\mathrm{3}{x}} =\mathrm{4}^{{log}\:\mathrm{4}{x}} \\ $$$${Taking}\:{logarthm}\:{of}\:{both}\:{sides} \\ $$$${log}\left(\mathrm{3}^{{log}\:\mathrm{3}{x}} \right)={log}\left(\mathrm{4}^{{log}\:\mathrm{4}{x}} \right) \\ $$$${log}\:\mathrm{3}{x}\:.{log}\:\mathrm{3}={log}\:\mathrm{4}{x}.{log}\:\mathrm{4} \\ $$$$\left({log}\:\mathrm{3}+{log}\:{x}\right).{log}\:\mathrm{3}=\left({log}\:\mathrm{4}+{log}\:{x}\right).{log}\:\mathrm{4} \\ $$$$\left({log}\:\mathrm{3}\right)^{\mathrm{2}} +{log}\:\mathrm{3}.{log}\:{x}=\left({log}\:\mathrm{4}\right)^{\mathrm{2}} +{log}\:\mathrm{4}.{log}\:{x} \\ $$$${log}\:\mathrm{4}.{log}\:{x}−{log}\:\mathrm{3}.{log}\:{x}=\left({log}\:\mathrm{3}\right)^{\mathrm{2}} −\left({log}\:\mathrm{4}\right)^{\mathrm{2}} \\ $$$${log}\:{x}.\left({log}\:\mathrm{4}−{log}\mathrm{3}\right)=\left({log}\:\mathrm{3}+{log}\:\mathrm{4}\right)\left({log}\:\mathrm{3}−{log}\:\mathrm{4}\right) \\ $$$$−{log}\:{x}\left({log}\:\mathrm{3}−{log}\:\mathrm{4}\right)=\left({log}\:\mathrm{3}+{log}\:\mathrm{4}\right)\left({log}\:\mathrm{3}−{log}\:\mathrm{4}\right) \\ $$$$−{log}\:{x}={log}\:\mathrm{3}\:+{log}\:\mathrm{4} \\ $$$${log}\:\left({x}^{−\mathrm{1}} \right)={log}\left(\mathrm{3}×\mathrm{4}\right) \\ $$$$\frac{\mathrm{1}}{{x}}=\mathrm{12} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{12}} \\ $$
