if-A-0-B-0-A-B-3-then-find-minimum-and-maximum-of-tan-A-tan-B-

Question Number 143858 by gsk2684 last updated on 19/Jun/21

if A ⩾ 0, B ⩾ 0, A + B = \frac{Π}{3} then

find minimum and maximum

of \tan A . \tan B

Answered by ajfour last updated on 19/Jun/21

\sqrt{3} = \frac{p + q}{1 - p q}

\Rightarrow 1 - p q = \frac{p + q}{\sqrt{3}}

p q = 1 - (\frac{p + q}{\sqrt{3}})

i f p = q

p^{2} + \frac{2 p}{\sqrt{3}} - 1 = 0

p = - \frac{1}{\sqrt{3}} \pm \frac{2}{\sqrt{3}}

p = \frac{1}{\sqrt{3}} \Rightarrow {(p q)}_{m a x} = \frac{1}{3}

{(p q)}_{m i n} = 0

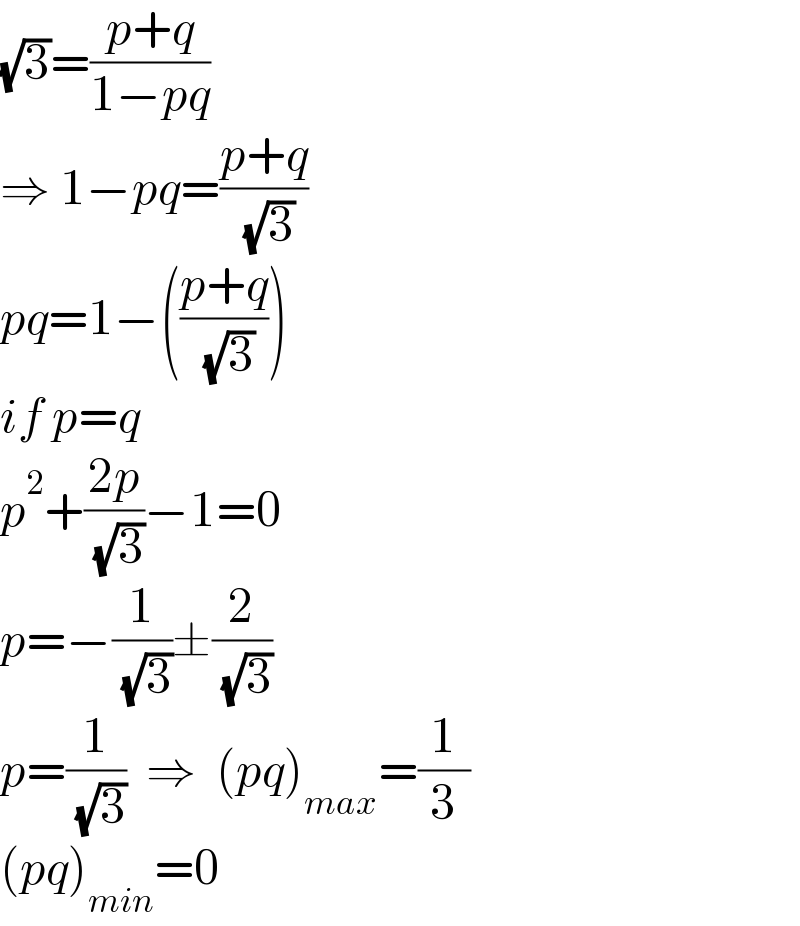
Commented by ajfour last updated on 19/Jun/21

A r e c t a n g l e o f g i v e n p e r i m e t e r

h a s m a x i m u m a r e a w h e n

i t i s a s q u a r e .

Commented by gsk2684 last updated on 19/Jun/21

thank you sir . i have a doubt

that why did you take p = q

Commented by gsk2684 last updated on 21/Jun/21

thanks alot .

Facebook Tweet Pin