Question Number 65971 by gunawan last updated on 07/Aug/19
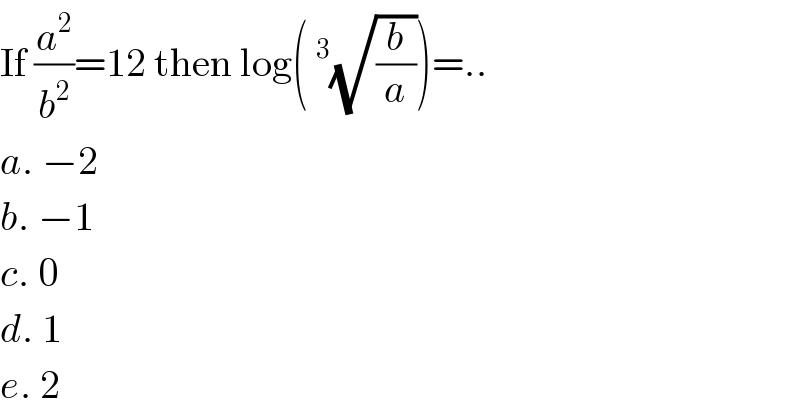
$$\mathrm{If}\:\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{12}\:\mathrm{then}\:\mathrm{log}\left(\:^{\mathrm{3}} \sqrt{\frac{{b}}{{a}}}\right)=.. \\ $$$${a}.\:−\mathrm{2} \\ $$$${b}.\:−\mathrm{1} \\ $$$${c}.\:\mathrm{0} \\ $$$${d}.\:\mathrm{1} \\ $$$${e}.\:\mathrm{2} \\ $$
Answered by MJS last updated on 07/Aug/19

$$\mathrm{ln}\:\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{12}}}\:=\mathrm{ln}\:\sqrt[{\mathrm{6}}]{\mathrm{12}}\:=\frac{\mathrm{ln}\:\mathrm{12}}{\mathrm{6}}=\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{6}} \\ $$
Answered by kaivan.ahmadi last updated on 07/Aug/19
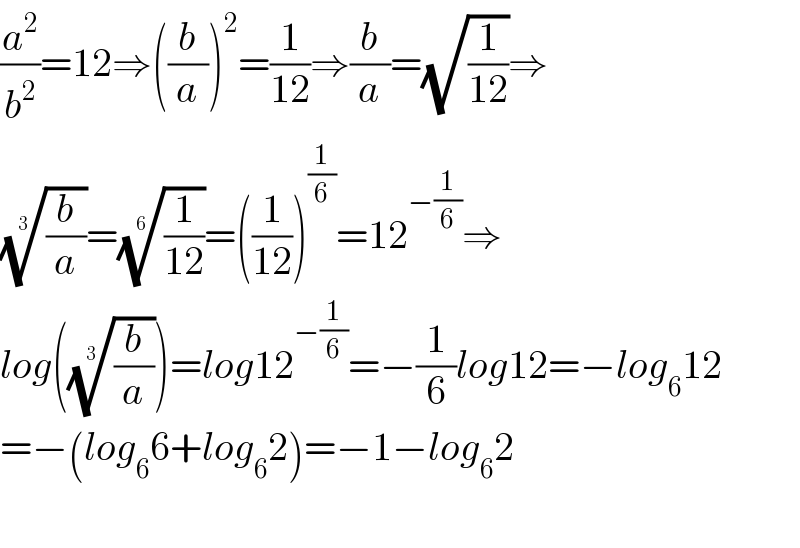
$$\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{12}\Rightarrow\left(\frac{{b}}{{a}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{12}}\Rightarrow\frac{{b}}{{a}}=\sqrt{\frac{\mathrm{1}}{\mathrm{12}}}\Rightarrow \\ $$$$\sqrt[{\mathrm{3}}]{\frac{{b}}{{a}}}=\sqrt[{\mathrm{6}}]{\frac{\mathrm{1}}{\mathrm{12}}}=\left(\frac{\mathrm{1}}{\mathrm{12}}\right)^{\frac{\mathrm{1}}{\mathrm{6}}} =\mathrm{12}^{−\frac{\mathrm{1}}{\mathrm{6}}} \Rightarrow \\ $$$${log}\left(\sqrt[{\mathrm{3}}]{\frac{{b}}{{a}}}\right)={log}\mathrm{12}^{−\frac{\mathrm{1}}{\mathrm{6}}} =−\frac{\mathrm{1}}{\mathrm{6}}{log}\mathrm{12}=−{log}_{\mathrm{6}} \mathrm{12} \\ $$$$=−\left({log}_{\mathrm{6}} \mathrm{6}+{log}_{\mathrm{6}} \mathrm{2}\right)=−\mathrm{1}−{log}_{\mathrm{6}} \mathrm{2} \\ $$$$ \\ $$
