Question Number 66276 by gunawan last updated on 12/Aug/19
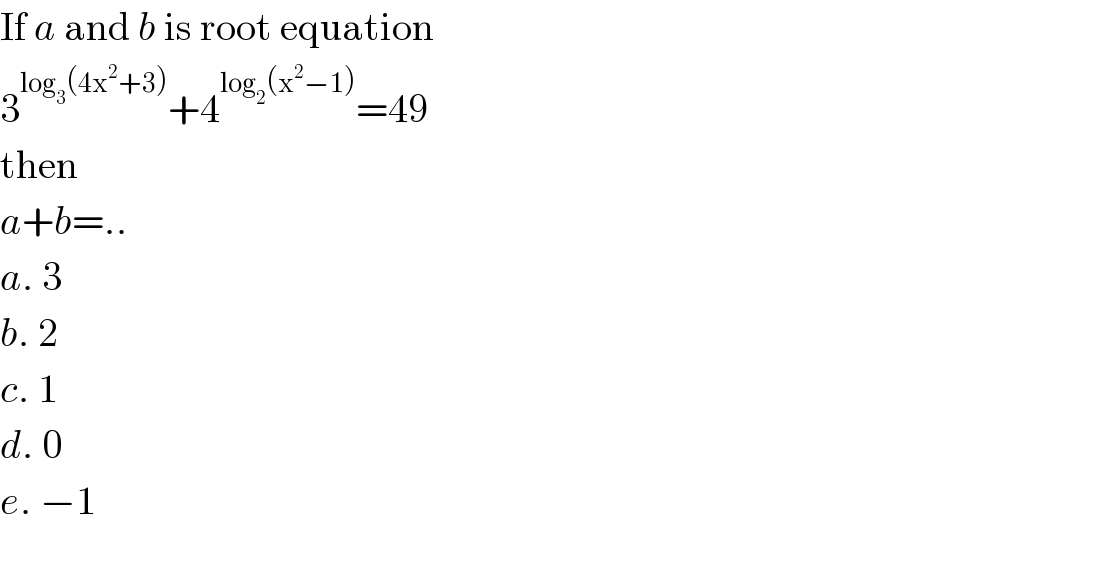
$$\mathrm{If}\:{a}\:\mathrm{and}\:{b}\:\mathrm{is}\:\mathrm{root}\:\mathrm{equation} \\ $$$$\mathrm{3}^{\mathrm{log}_{\mathrm{3}} \left(\mathrm{4x}^{\mathrm{2}} +\mathrm{3}\right)} +\mathrm{4}^{\mathrm{log}_{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)} =\mathrm{49} \\ $$$$\mathrm{then} \\ $$$${a}+{b}=.. \\ $$$${a}.\:\mathrm{3} \\ $$$${b}.\:\mathrm{2} \\ $$$${c}.\:\mathrm{1} \\ $$$${d}.\:\mathrm{0} \\ $$$${e}.\:−\mathrm{1} \\ $$$$ \\ $$
Answered by Kunal12588 last updated on 12/Aug/19
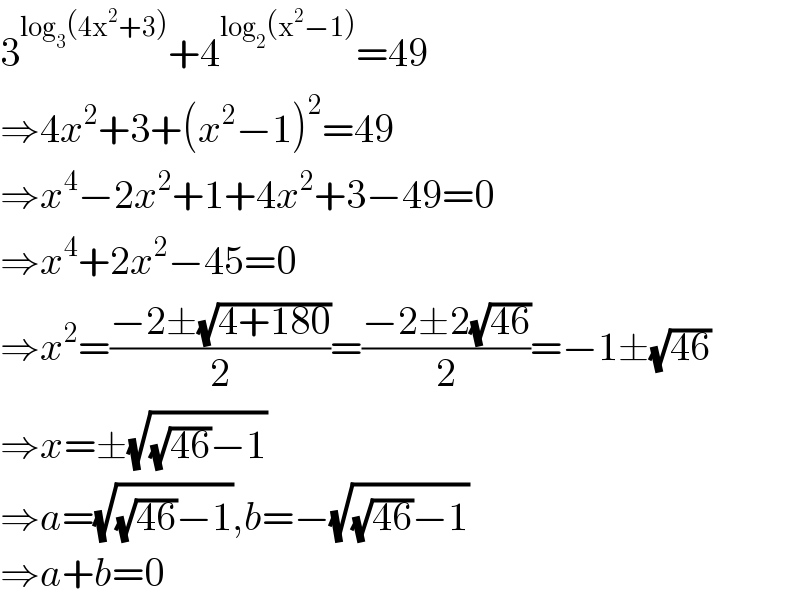
$$\mathrm{3}^{\mathrm{log}_{\mathrm{3}} \left(\mathrm{4x}^{\mathrm{2}} +\mathrm{3}\right)} +\mathrm{4}^{\mathrm{log}_{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)} =\mathrm{49} \\ $$$$\Rightarrow\mathrm{4}{x}^{\mathrm{2}} +\mathrm{3}+\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} =\mathrm{49} \\ $$$$\Rightarrow{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} +\mathrm{3}−\mathrm{49}=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{45}=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} =\frac{−\mathrm{2}\pm\sqrt{\mathrm{4}+\mathrm{180}}}{\mathrm{2}}=\frac{−\mathrm{2}\pm\mathrm{2}\sqrt{\mathrm{46}}}{\mathrm{2}}=−\mathrm{1}\pm\sqrt{\mathrm{46}} \\ $$$$\Rightarrow{x}=\pm\sqrt{\sqrt{\mathrm{46}}−\mathrm{1}} \\ $$$$\Rightarrow{a}=\sqrt{\sqrt{\mathrm{46}}−\mathrm{1}},{b}=−\sqrt{\sqrt{\mathrm{46}}−\mathrm{1}} \\ $$$$\Rightarrow{a}+{b}=\mathrm{0} \\ $$
Commented by gunawan last updated on 12/Aug/19

$$\mathrm{thanks}\:\mathrm{Sir} \\ $$
