Menu Close

If-a-b-and-c-are-integers-not-all-simultaneously-equal-and-w-1-is-a-cube-root-of-unity-then-the-minimum-value-of-a-bw-cw-2-is-A-0-B-1-C-3-2-D-1-2-

Tinku Tara 0 Comments
Pin




Question Number 139590 by EnterUsername last updated on 29/Apr/21
If a, b and c are integers not all simultaneously equal and w≠1 is a cube root of unity, then the minimum value of ∣a+bw+cw^2 ∣ is (A) 0 (B) 1 (C) (√3)/2 (D) 1/2
$$\mathrm{If}\:{a},\:{b}\:\mathrm{and}\:{c}\:\mathrm{are}\:\mathrm{integers}\:\mathrm{not}\:\mathrm{all}\:\mathrm{simultaneously}\:\mathrm{equal} \\ $$$$\mathrm{and}\:{w}\neq\mathrm{1}\:\mathrm{is}\:\mathrm{a}\:\mathrm{cube}\:\mathrm{root}\:\mathrm{of}\:\mathrm{unity},\:\mathrm{then}\:\mathrm{the}\:\mathrm{minimum} \\ $$$$\mathrm{value}\:\mathrm{of}\:\mid{a}+{bw}+{cw}^{\mathrm{2}} \mid\:\mathrm{is}\: \\ $$$$\left(\mathrm{A}\right)\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\left(\mathrm{B}\right)\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\left(\mathrm{C}\right)\:\sqrt{\mathrm{3}}/\mathrm{2}\:\:\:\:\:\:\:\:\:\:\left(\mathrm{D}\right)\:\mathrm{1}/\mathrm{2} \\ $$
Answered by MJS_new last updated on 29/Apr/21
∣a+bw+cw^2 ∣= [w=−(1/2)±((√3)/2)i] =(√(a^2 +b^2 +c^2 −(ab+ac+bc)))=A (a, b, c) (d/dc)[A (a, b, c)]=0 ⇒ c=((a+b)/2) A (a, b, ((a+b)/2)) =((√3)/2)∣a−b∣ since b=a ⇒ c=a is not allowed and a,b ∈Z the minimum is at ∣a−b∣=1 ⇒ answer is ((√3)/2)
$$\mid{a}+{bw}+{cw}^{\mathrm{2}} \mid= \\ $$$$\:\:\:\:\:\left[{w}=−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right] \\ $$$$=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\left({ab}+{ac}+{bc}\right)}={A}\:\left({a},\:{b},\:{c}\right) \\ $$$$\frac{{d}}{{dc}}\left[{A}\:\left({a},\:{b},\:{c}\right)\right]=\mathrm{0}\:\Rightarrow\:{c}=\frac{{a}+{b}}{\mathrm{2}} \\ $$$${A}\:\left({a},\:{b},\:\frac{{a}+{b}}{\mathrm{2}}\right)\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mid{a}−{b}\mid \\ $$$$\mathrm{since}\:{b}={a}\:\Rightarrow\:{c}={a}\:\mathrm{is}\:\mathrm{not}\:\mathrm{allowed}\:\mathrm{and}\:{a},{b}\:\in\mathbb{Z} \\ $$$$\mathrm{the}\:\mathrm{minimum}\:\mathrm{is}\:\mathrm{at}\:\mid{a}−{b}\mid=\mathrm{1}\:\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$
Commented by EnterUsername last updated on 29/Apr/21
Thanks Sir. I′ve understood your method. But author′s choice is (B). Do you think it′s a mistake ?
$$\mathrm{Thanks}\:\mathrm{Sir}.\:\mathrm{I}'\mathrm{ve}\:\mathrm{understood}\:\mathrm{your}\:\mathrm{method}.\:\mathrm{But}\:\mathrm{author}'\mathrm{s} \\ $$$$\mathrm{choice}\:\mathrm{is}\:\left(\mathrm{B}\right).\:\mathrm{Do}\:\mathrm{you}\:\mathrm{think}\:\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{mistake}\:? \\ $$
Commented by EnterUsername last updated on 29/Apr/21
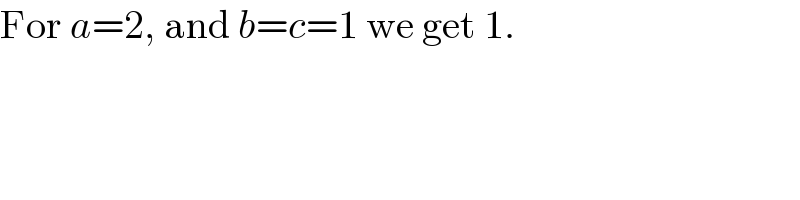
For a=2, and b=c=1 we get 1.
$$\mathrm{For}\:{a}=\mathrm{2},\:\mathrm{and}\:{b}={c}=\mathrm{1}\:\mathrm{we}\:\mathrm{get}\:\mathrm{1}. \\ $$
Commented by MJS_new last updated on 29/Apr/21
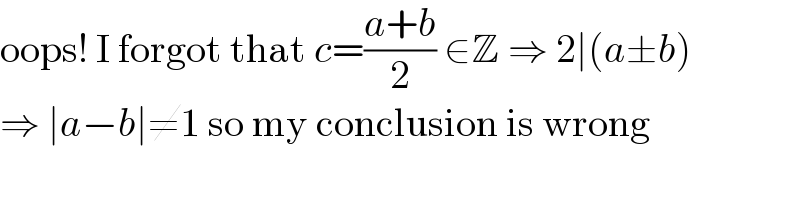
oops! I forgot that c=((a+b)/2) ∈Z ⇒ 2∣(a±b) ⇒ ∣a−b∣≠1 so my conclusion is wrong
$$\mathrm{oops}!\:\mathrm{I}\:\mathrm{forgot}\:\mathrm{that}\:{c}=\frac{{a}+{b}}{\mathrm{2}}\:\in\mathbb{Z}\:\Rightarrow\:\mathrm{2}\mid\left({a}\pm{b}\right) \\ $$$$\Rightarrow\:\mid{a}−{b}\mid\neq\mathrm{1}\:\mathrm{so}\:\mathrm{my}\:\mathrm{conclusion}\:\mathrm{is}\:\mathrm{wrong} \\ $$
Commented by EnterUsername last updated on 29/Apr/21
OK. Thank you Sir 😃
$$\mathrm{OK}.\:\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$😃
Commented by mr W last updated on 29/Apr/21
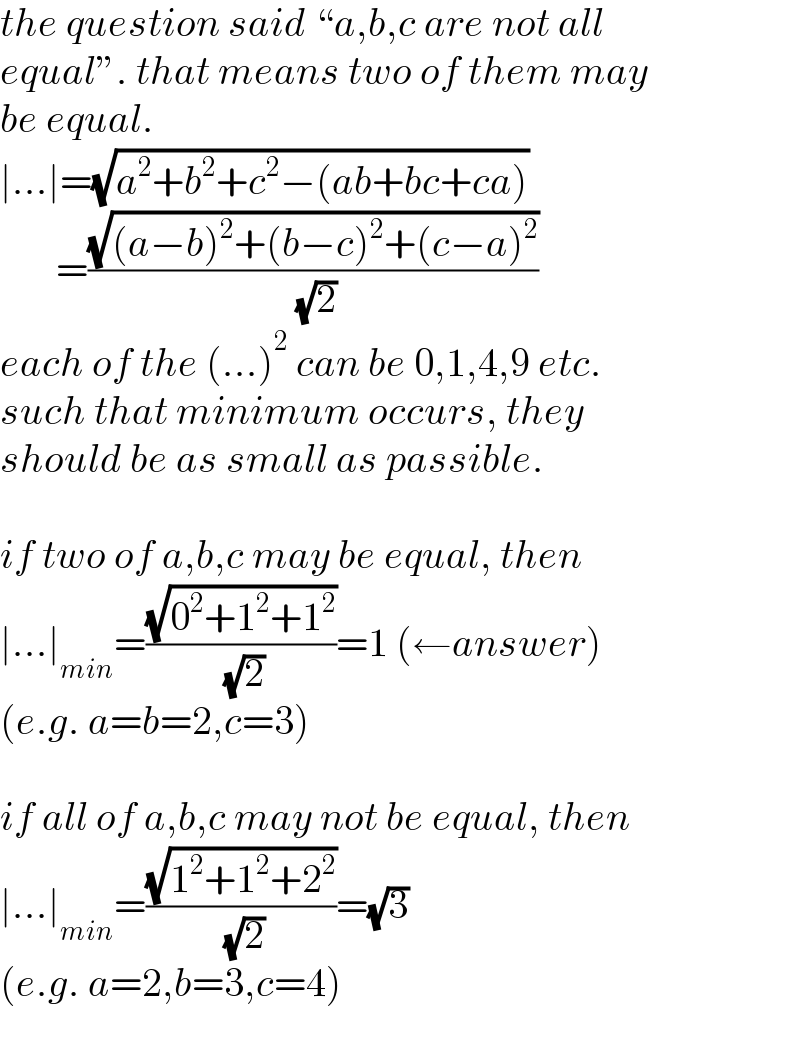
the question said “a,b,c are not all equal”. that means two of them may be equal. ∣...∣=(√(a^2 +b^2 +c^2 −(ab+bc+ca))) =((√((a−b)^2 +(b−c)^2 +(c−a)^2 ))/( (√2))) each of the (...)^2 can be 0,1,4,9 etc. such that minimum occurs, they should be as small as passible. if two of a,b,c may be equal, then ∣...∣_(min) =((√(0^2 +1^2 +1^2 ))/( (√2)))=1 (←answer) (e.g. a=b=2,c=3) if all of a,b,c may not be equal, then ∣...∣_(min) =((√(1^2 +1^2 +2^2 ))/( (√2)))=(√3) (e.g. a=2,b=3,c=4)
$${the}\:{question}\:{said}\:“{a},{b},{c}\:{are}\:{not}\:{all} \\ $$$${equal}''.\:{that}\:{means}\:{two}\:{of}\:{them}\:{may} \\ $$$${be}\:{equal}. \\ $$$$\mid…\mid=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\left({ab}+{bc}+{ca}\right)} \\ $$$$\:\:\:\:\:\:\:=\frac{\sqrt{\left({a}−{b}\right)^{\mathrm{2}} +\left({b}−{c}\right)^{\mathrm{2}} +\left({c}−{a}\right)^{\mathrm{2}} }}{\:\sqrt{\mathrm{2}}} \\ $$$${each}\:{of}\:{the}\:\left(…\right)^{\mathrm{2}} \:{can}\:{be}\:\mathrm{0},\mathrm{1},\mathrm{4},\mathrm{9}\:{etc}. \\ $$$${such}\:{that}\:{minimum}\:{occurs},\:{they} \\ $$$${should}\:{be}\:{as}\:{small}\:{as}\:{passible}.\: \\ $$$$ \\ $$$${if}\:{two}\:{of}\:{a},{b},{c}\:{may}\:{be}\:{equal},\:{then} \\ $$$$\mid…\mid_{{min}} =\frac{\sqrt{\mathrm{0}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }}{\:\sqrt{\mathrm{2}}}=\mathrm{1}\:\left(\leftarrow{answer}\right) \\ $$$$\left({e}.{g}.\:{a}={b}=\mathrm{2},{c}=\mathrm{3}\right) \\ $$$$ \\ $$$${if}\:{all}\:{of}\:{a},{b},{c}\:{may}\:{not}\:{be}\:{equal},\:{then} \\ $$$$\mid…\mid_{{min}} =\frac{\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }}{\:\sqrt{\mathrm{2}}}=\sqrt{\mathrm{3}} \\ $$$$\left({e}.{g}.\:{a}=\mathrm{2},{b}=\mathrm{3},{c}=\mathrm{4}\right) \\ $$
Commented by EnterUsername last updated on 29/Apr/21
Thank you Sir !
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}\:! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *