If-a-b-c-and-a-2-b-c-b-2-c-a-c-2-a-b-12-a-b-c-a-b-c-b-a-c-c-a-b-4-3-then-find-a-b-c-

Question Number 70598 by Shamim last updated on 06/Oct/19

If a, b, c \in ℜ and \frac{a^{2}}{b + c} + \frac{b^{2}}{c + a} + \frac{c^{2}}{a + b} = \frac{12}{a + b + c}

, \frac{a}{b + c} + \frac{b}{a + c} + \frac{c}{a + b} = \frac{4}{3} then find a + b + c = ?

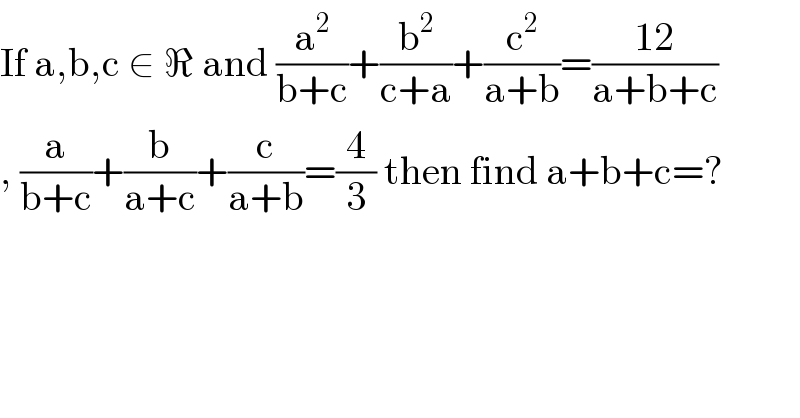
Answered by som(math1967) last updated on 06/Oct/19

\frac{a^{2}}{b + c} + a + \frac{b^{2}}{c + a} + b + \frac{c^{2}}{c + a} + c - (a + b + c)

= \frac{12}{a + b + c}

\frac{a (a + b + c)}{b + c} + \frac{b (a + b + c)}{c + a} + \frac{c (a + b + c)}{a + b}

- (a + b + c) = \frac{12}{a + b + c}

(a + b + c) (\frac{a}{b + c} + \frac{b}{c + a} + \frac{c}{a + b} - 1) = \frac{12}{a + b + c}

(a + b + c) (\frac{4}{3} - 1) = \frac{12}{a + b + c} ★

\frac{{(a + b + c)}^{2}}{3} = 12

{(a + b + c)}^{2} = 36 \Rightarrow (a + b + c) = \pm 6

★ \frac{a}{b + c} + \frac{b}{c + a} + \frac{c}{a + b} = \frac{4}{3}

Commented by Shamim last updated on 06/Oct/19

tnks

Commented by Rasheed.Sindhi last updated on 06/Oct/19

\lor ⊓ ∣ ⊏\in!

Commented by som(math1967) last updated on 06/Oct/19

N i c e u s e o f m a t h e m a t i c a l s y m b o l s

Commented by peter frank last updated on 06/Oct/19

g o o d