Question Number 131505 by benjo_mathlover last updated on 05/Feb/21
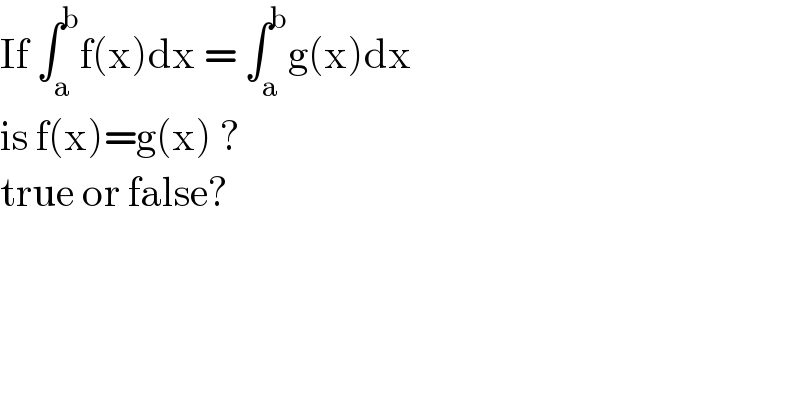
$$\mathrm{If}\:\int_{\mathrm{a}} ^{\mathrm{b}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:=\:\int_{\mathrm{a}} ^{\mathrm{b}} \mathrm{g}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{is}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{g}\left(\mathrm{x}\right)\:?\: \\ $$$$\mathrm{true}\:\mathrm{or}\:\mathrm{false}? \\ $$
Commented by EDWIN88 last updated on 05/Feb/21

$$\mathrm{If}\:\underset{\mathrm{a}} {\overset{\mathrm{b}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:=\:\underset{\mathrm{a}} {\overset{\mathrm{b}} {\int}}\mathrm{g}\left(\mathrm{x}\right)\mathrm{dx}\:,\:\mathrm{we}\:\mathrm{does}\:\mathrm{not}\:\mathrm{claim}\:\mathrm{that}\: \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{g}\left(\mathrm{x}\right).\:\mathrm{but}\:\underset{\mathrm{a}} {\overset{\mathrm{b}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:=\:\underset{\mathrm{a}} {\overset{\mathrm{b}} {\int}}\mathrm{f}\left(\mathrm{a}+\mathrm{b}−\mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{then}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{a}+\mathrm{b}−\mathrm{x}\right). \\ $$
Answered by talminator2856791 last updated on 05/Feb/21

$$\:\mathrm{false} \\ $$
Answered by talminator2856791 last updated on 05/Feb/21

$$\:\mathrm{take}\:\mathrm{any}\:\mathrm{two}\:\mathrm{straight}\:\mathrm{lines}\:{f}\left({x}\right),\:{g}\left({x}\right)\:\mathrm{of}\:\mathrm{different}\:\mathrm{gradients}.\:\:\:\:\:\:\:\: \\ $$$$\:\mathrm{from}\:\mathrm{point}\:\mathrm{of}\:\mathrm{intersection}\:\left({m};{n}\right),\:\mathrm{take}\:\mathrm{any}\:\mathrm{real}\:{p}\:\:\mathrm{such}\:\mathrm{that} \\ $$$$\:\mid{f}\left({p}\right)\mid,\:\mid{g}\left({p}\right)\mid\:\leqslant\:\mid{n}\mid,\:\:\mathrm{then} \\ $$$$\:\:\:\:\:\:\:\:\int_{{m}−{p}} ^{\:{m}+{p}} {f}\left({x}\right){dx}\:=\:\int_{{m}−{p}} ^{\:{m}+{p}} {g}\left({x}\right){dx} \\ $$$$\:\Rightarrow\:\int_{{a}} ^{\:{b}} {f}\left({x}\right){dx}\:=\:\int_{{a}} ^{\:{b}} {g}\left({x}\right){dx} \\ $$$$\:\mathrm{the}\:\mathrm{assertion}\:\mathrm{that}\:{f}\left({x}\right)\:=\:{g}\left({x}\right)\:\mathrm{is}\:\mathrm{false},\:\mathrm{as}\:{f}\left({x}\right)\:\mathrm{and}\:{g}\left({x}\right) \\ $$$$\:\mathrm{can}\:\mathrm{not}\:\mathrm{be}\:\mathrm{the}\:\mathrm{same}\:\mathrm{line}\:\mathrm{if}\:\mathrm{their}\:\mathrm{gradients}\:\mathrm{are}\:\mathrm{different}. \\ $$$$\: \\ $$
Commented by benjo_mathlover last updated on 05/Feb/21

$$\mathrm{give}\:\mathrm{me}\:\mathrm{a}\:\mathrm{counterexample} \\ $$
Answered by TheSupreme last updated on 05/Feb/21

$${c}=\frac{\int_{{a}} ^{{b}} {f}\left({x}\right){dx}}{{b}−{a}} \\ $$$${g}\left({x}\right)={c}\: \\ $$$${f}\left({x}\right)={any}\:{function} \\ $$$${f}\left({x}\right)\neq{c} \\ $$
Commented by talminator2856791 last updated on 05/Feb/21
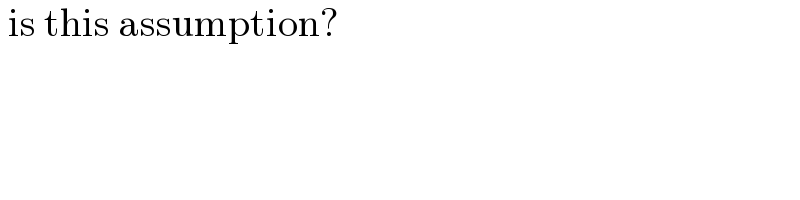
$$\:\mathrm{is}\:\mathrm{this}\:\mathrm{assumption}? \\ $$
Answered by mr W last updated on 05/Feb/21

Commented by prakash jain last updated on 05/Feb/21

$$\mathrm{If}\:\int_{{a}} ^{{b}} {f}\left({x}\right){dx}=\int_{{a}} ^{{b}} {g}\left({x}\right){dx} \\ $$$$\mathrm{for}\:\mathrm{all}\:{a},{b}\:\in\:\mathbb{R}\:\mathrm{then}\:{f}\left({x}\right)={g}\left({x}\right) \\ $$$$\mathrm{correct}? \\ $$
Commented by mr W last updated on 05/Feb/21

$${yes},\:{i}\:{think}. \\ $$$${if}\:\int_{{a}} ^{{b}} {f}\left({x}\right){dx}=\int_{{a}} ^{{b}} {g}\left({x}\right){dx}\:{for}\:{any}\:{a},{b}\in{R} \\ $$$$\Rightarrow\underset{{b}\rightarrow{a}} {\mathrm{lim}}\int_{{a}} ^{{b}} {f}\left({x}\right){dx}=\underset{{b}\rightarrow{a}} {\mathrm{lim}}\int_{{a}} ^{{b}} {g}\left({x}\right){dx} \\ $$$$\Rightarrow\underset{{b}\rightarrow{a}} {\mathrm{lim}}{f}\left({a}\right)\left({b}−{a}\right)=\underset{{b}\rightarrow{a}} {\mathrm{lim}}{g}\left({a}\right)\left({b}−{a}\right) \\ $$$$\Rightarrow{f}\left({a}\right)={g}\left({a}\right) \\ $$$$\Rightarrow{f}\left({x}\right)={g}\left({x}\right) \\ $$
Commented by mr W last updated on 05/Feb/21

$$\int_{{a}} ^{{b}} {f}\left({x}\right){dx}={red}\:{shaded}\:{area}\: \\ $$$$\int_{{a}} ^{{b}} {g}\left({x}\right){dx}={blue}\:{shaded}\:{area}\: \\ $$$$\int_{{a}} ^{{b}} {f}\left({x}\right){dx}=\int_{{a}} ^{{b}} {g}\left({x}\right){dx}\:{means}\:{only} \\ $$$${that}\:{the}\:{red}\:{shaded}\:{area}\:{and}\:{the} \\ $$$${blue}\:{shaded}\:{area}\:{are}\:{equal}.\:{it}\:{doesn}'{t} \\ $$$${mean}\:{that}\:{f}\left({x}\right)={g}\left({x}\right)! \\ $$
