Question Number 7294 by Tawakalitu. last updated on 21/Aug/16
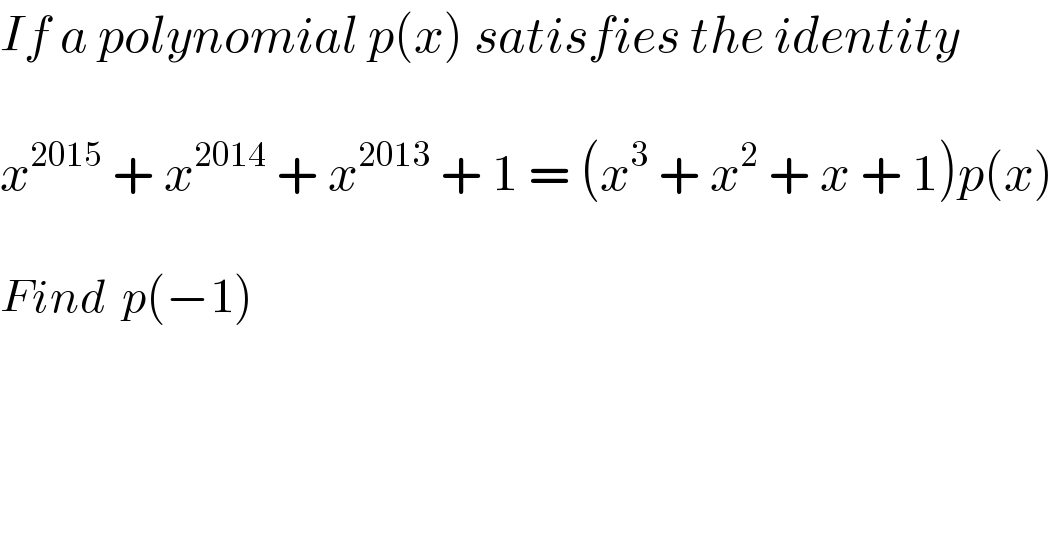
$${If}\:{a}\:{polynomial}\:{p}\left({x}\right)\:{satisfies}\:{the}\:{identity} \\ $$$$ \\ $$$${x}^{\mathrm{2015}} \:+\:{x}^{\mathrm{2014}} \:+\:{x}^{\mathrm{2013}} \:+\:\mathrm{1}\:=\:\left({x}^{\mathrm{3}} \:+\:{x}^{\mathrm{2}} \:+\:{x}\:+\:\mathrm{1}\right){p}\left({x}\right) \\ $$$$ \\ $$$${Find}\:\:{p}\left(−\mathrm{1}\right) \\ $$
Commented by prakash jain last updated on 21/Aug/16
![p(x)=((x^(2015) +x^(2014) +x^(2013) +1)/(x^3 +x^2 +x+1)) =(((x^(2015) +x^(2014) +x^(2013) +x^(2012) +1−x^(2012) ))/(x^3 +x^2 +x+1)) =x^(2012) −((x^(2012) −1)/(x^3 +x^2 +x+1)) =x^(2012) −(((x−1)(x^(2012) −1))/(x^4 −1)) =x^(2012) −(x−1)(([(x^4 )^(503) −1])/(x^4 −1)) =x^(2012) −(x−1)Σ_(i=0) ^(502) (x^4 )^i p(−1)=(−1)^(2012) −(−1−1)Σ_(i=0) ^(502) (1)^i =1+2(503)=1+1006=1007](https://www.tinkutara.com/question/Q7295.png)
$${p}\left({x}\right)=\frac{{x}^{\mathrm{2015}} +{x}^{\mathrm{2014}} +{x}^{\mathrm{2013}} +\mathrm{1}}{{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1}} \\ $$$$=\frac{\left({x}^{\mathrm{2015}} +{x}^{\mathrm{2014}} +{x}^{\mathrm{2013}} +{x}^{\mathrm{2012}} +\mathrm{1}−{x}^{\mathrm{2012}} \right)}{{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1}} \\ $$$$={x}^{\mathrm{2012}} −\frac{{x}^{\mathrm{2012}} −\mathrm{1}}{{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1}} \\ $$$$={x}^{\mathrm{2012}} −\frac{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2012}} −\mathrm{1}\right)}{{x}^{\mathrm{4}} −\mathrm{1}} \\ $$$$={x}^{\mathrm{2012}} −\left({x}−\mathrm{1}\right)\frac{\left[\left({x}^{\mathrm{4}} \right)^{\mathrm{503}} −\mathrm{1}\right]}{{x}^{\mathrm{4}} −\mathrm{1}} \\ $$$$={x}^{\mathrm{2012}} −\left({x}−\mathrm{1}\right)\underset{{i}=\mathrm{0}} {\overset{\mathrm{502}} {\sum}}\left({x}^{\mathrm{4}} \right)^{{i}} \\ $$$${p}\left(−\mathrm{1}\right)=\left(−\mathrm{1}\right)^{\mathrm{2012}} −\left(−\mathrm{1}−\mathrm{1}\right)\underset{{i}=\mathrm{0}} {\overset{\mathrm{502}} {\sum}}\left(\mathrm{1}\right)^{{i}} \\ $$$$=\mathrm{1}+\mathrm{2}\left(\mathrm{503}\right)=\mathrm{1}+\mathrm{1006}=\mathrm{1007} \\ $$
Commented by Tawakalitu. last updated on 22/Aug/16
$${Thanks}\:{so}\:{much}\:{sir}.\:{i}\:{really}\:{appreciate}. \\ $$
Commented by peter james last updated on 22/Aug/16

$${Nice}\:{working}… \\ $$
