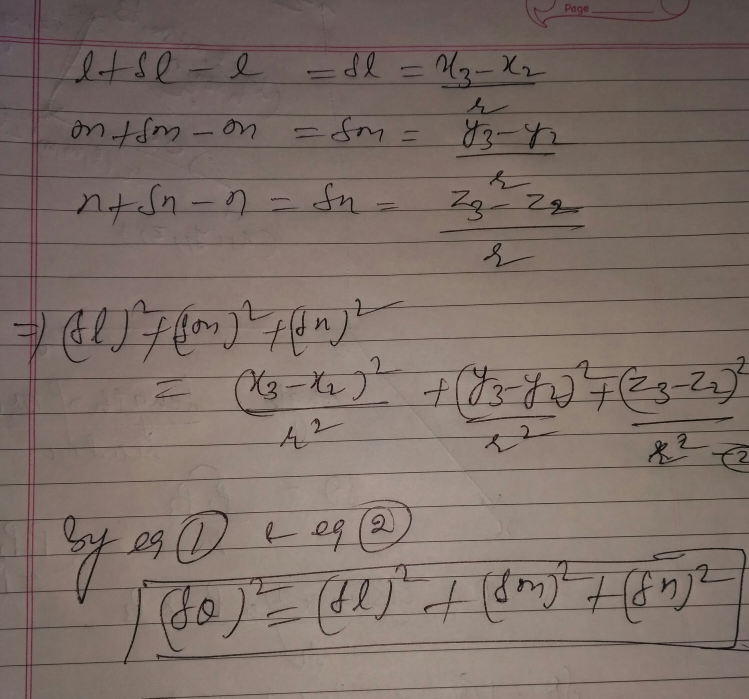Question Number 75445 by vishalbhardwaj last updated on 11/Dec/19
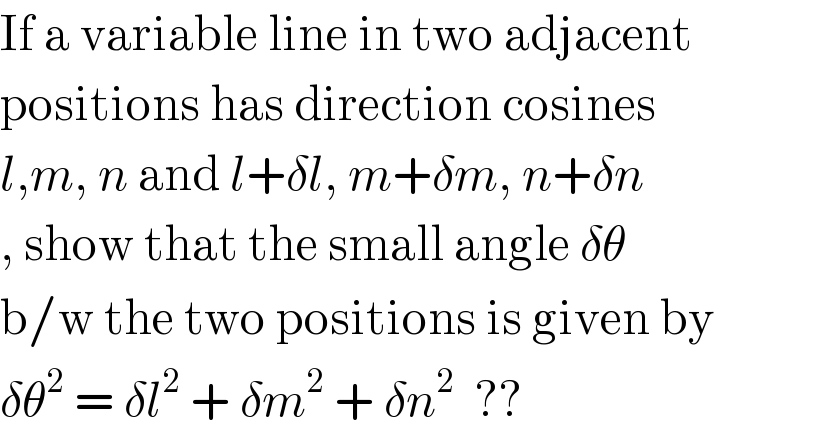
Answered by mr W last updated on 11/Dec/19
![x_1 =l y_1 =m z_1 =n x_2 =l+δl y_2 =m+δm z_2 =n+δn (Δl)^2 =(Δx)^2 +(Δy)^2 +(Δz)^2 =(x_2 −x_1 )^2 +(y_2 −y_1 )^2 +(z_2 −z_2 )^2 =(δl)^2 +(δm)^2 +(δn)^2 ...(i) (Δl)^2 =1^2 +1^2 −2×1×1×cos (δθ) =2−2 [1−2 sin^2 (((δθ)/2))] =4 [sin ((δθ)/2)]^2 ≈4 [((δθ)/2)]^2 =(δθ)^2 ...(ii) ⇒(δθ)^2 =(δl)^2 +(δm)^2 +(δn)^2](https://www.tinkutara.com/question/Q75448.png)
Commented by mr W last updated on 11/Dec/19
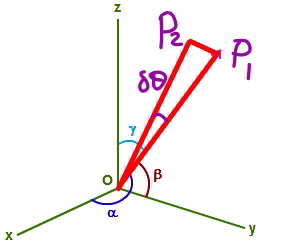
Commented by mr W last updated on 11/Dec/19
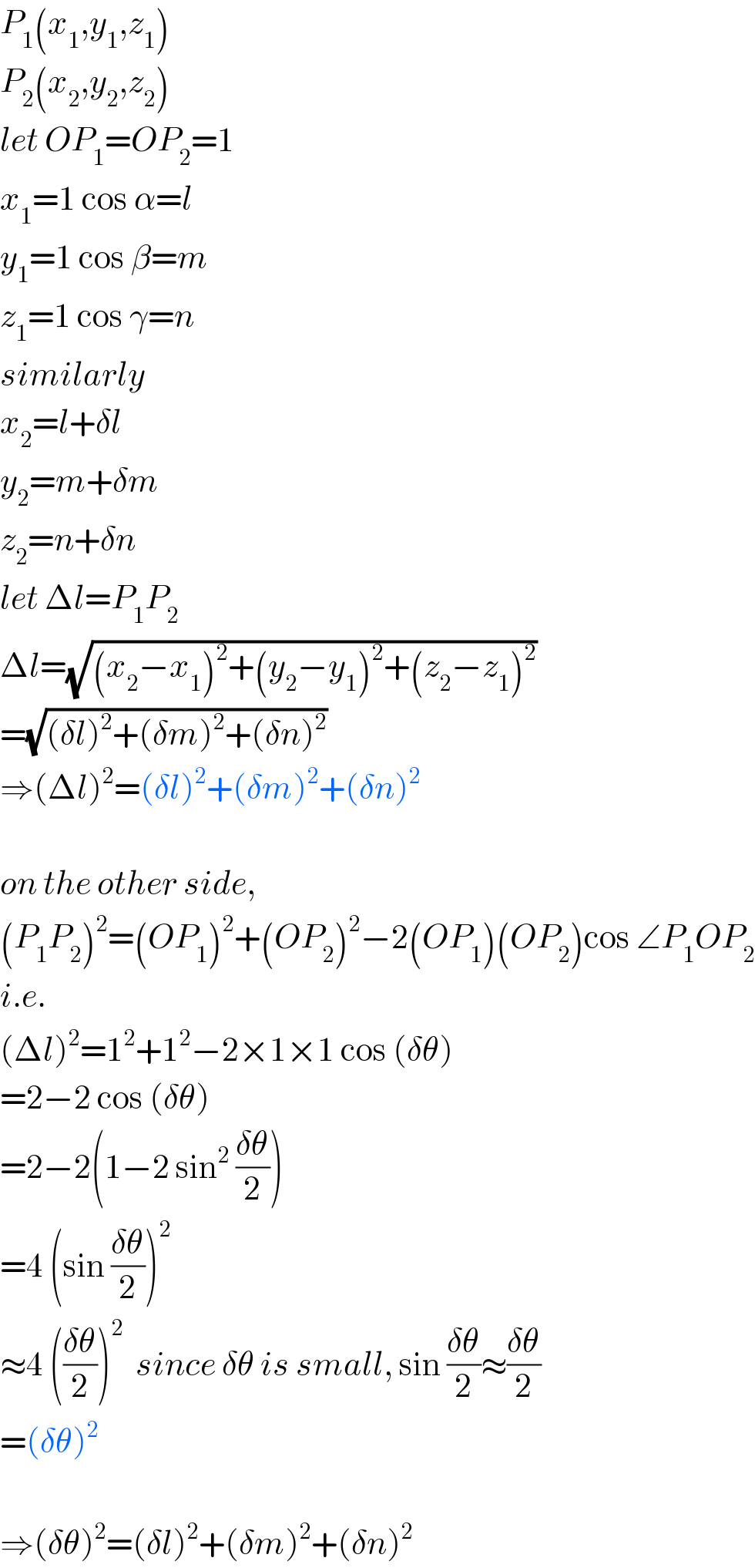
Commented by vishalbhardwaj last updated on 11/Dec/19

Commented by peter frank last updated on 11/Dec/19

Commented by vishalbhardwaj last updated on 11/Dec/19

Commented by vishalbhardwaj last updated on 12/Dec/19

Commented by mr W last updated on 12/Dec/19

Commented by mr W last updated on 12/Dec/19
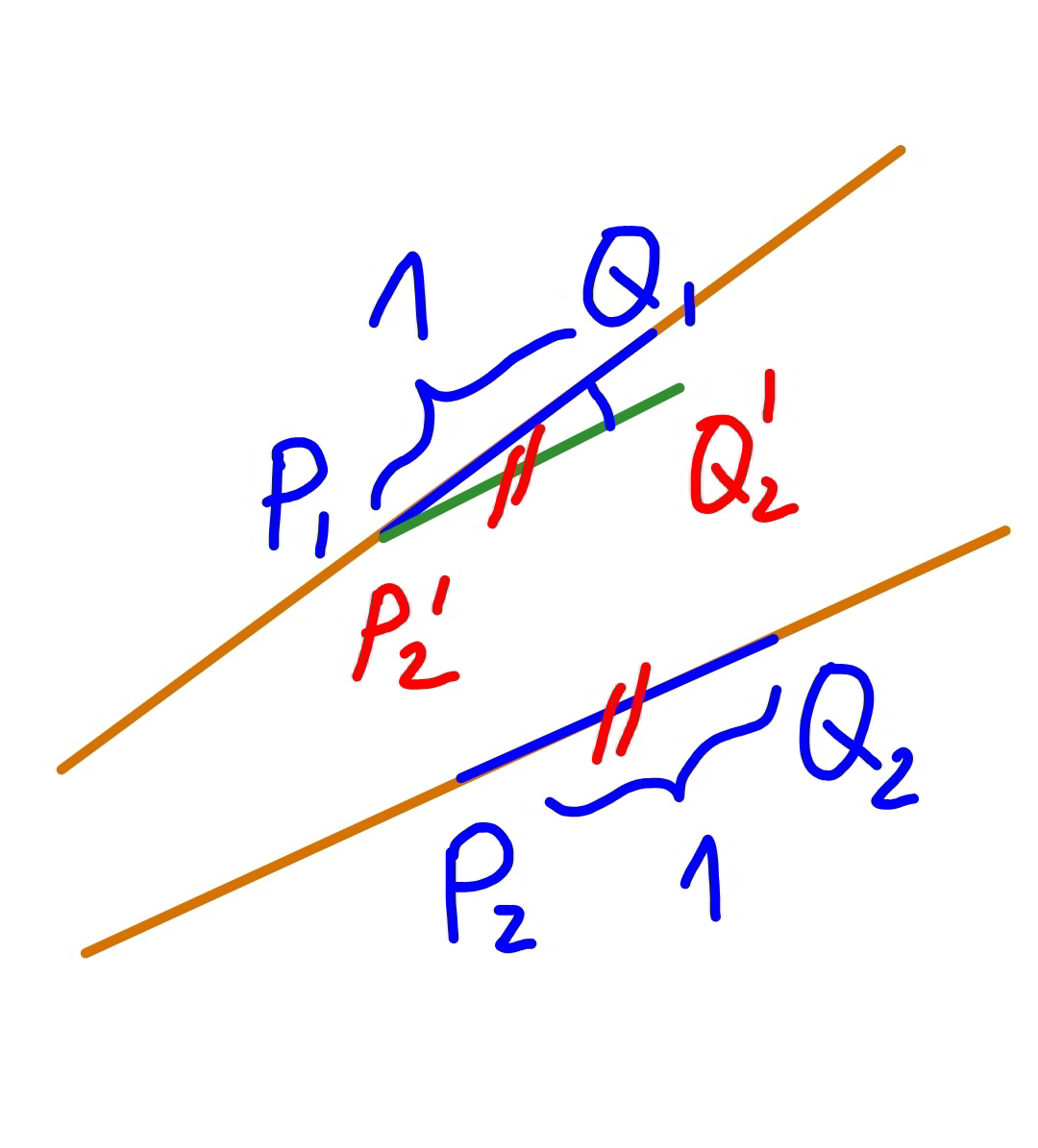
Commented by vishalbhardwaj last updated on 12/Dec/19

Commented by mr W last updated on 12/Dec/19

Answered by vishalbhardwaj last updated on 12/Dec/19

Answered by vishalbhardwaj last updated on 12/Dec/19