Menu Close

If-and-are-different-complex-numbers-with-1-then-1-

Tinku Tara 0 Comments
Pin




Question Number 1331 by a@b.c last updated on 23/Jul/15
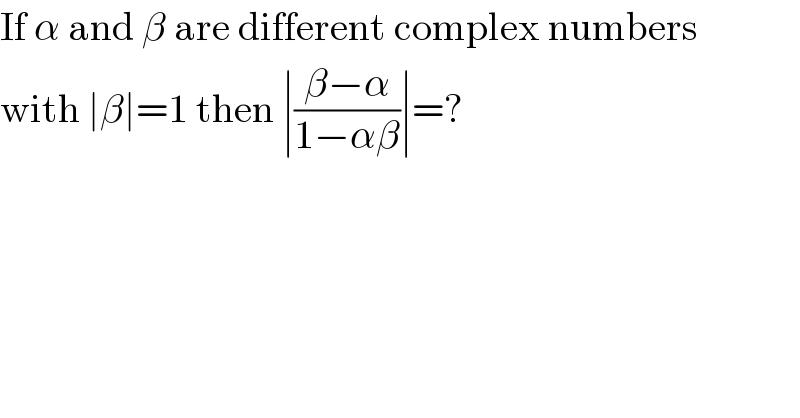
If α and β are different complex numbers with ∣β∣=1 then ∣((β−α)/(1−αβ))∣=?
$$\mathrm{If}\:\alpha\:\mathrm{and}\:\beta\:\mathrm{are}\:\mathrm{different}\:\mathrm{complex}\:\mathrm{numbers} \\ $$$$\mathrm{with}\:\mid\beta\mid=\mathrm{1}\:\mathrm{then}\:\mid\frac{\beta−\alpha}{\mathrm{1}−\alpha\beta}\mid=? \\ $$
Commented by 123456 last updated on 23/Jul/15
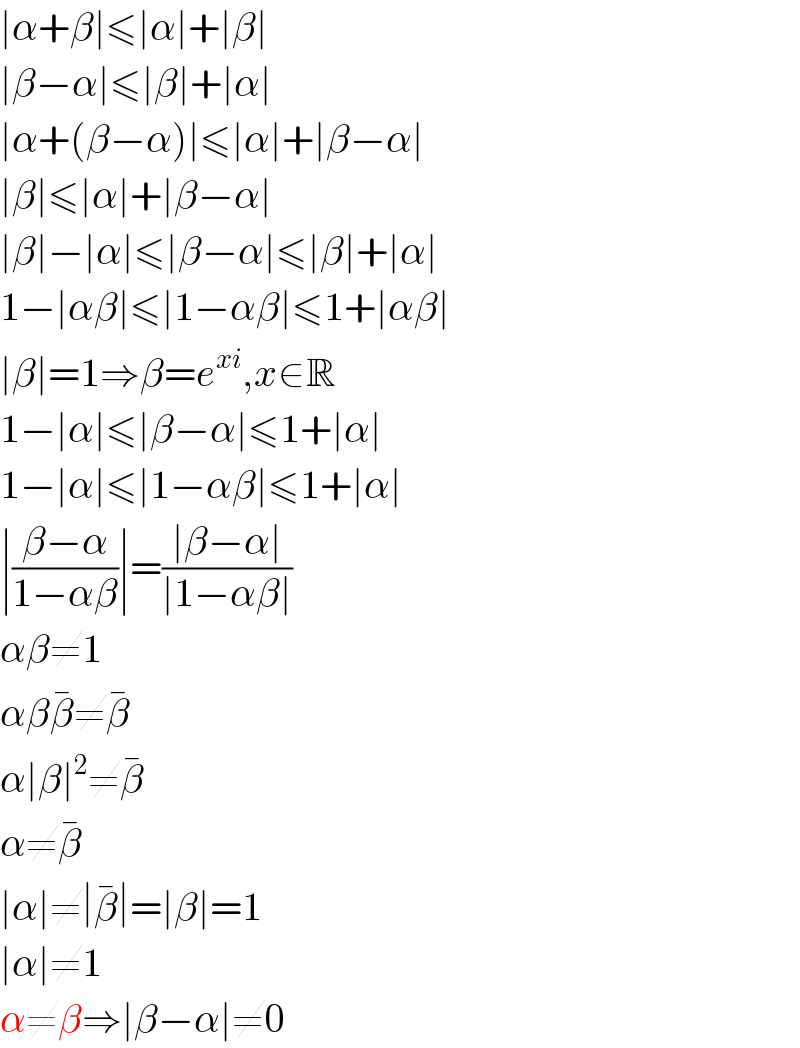
∣α+β∣≤∣α∣+∣β∣ ∣β−α∣≤∣β∣+∣α∣ ∣α+(β−α)∣≤∣α∣+∣β−α∣ ∣β∣≤∣α∣+∣β−α∣ ∣β∣−∣α∣≤∣β−α∣≤∣β∣+∣α∣ 1−∣αβ∣≤∣1−αβ∣≤1+∣αβ∣ ∣β∣=1⇒β=e^(xi) ,x∈R 1−∣α∣≤∣β−α∣≤1+∣α∣ 1−∣α∣≤∣1−αβ∣≤1+∣α∣ ∣((β−α)/(1−αβ))∣=((∣β−α∣)/(∣1−αβ∣)) αβ≠1 αββ^� ≠β^� α∣β∣^2 ≠β^� α≠β^� ∣α∣≠∣β^� ∣=∣β∣=1 ∣α∣≠1 α≠β⇒∣β−α∣≠0
$$\mid\alpha+\beta\mid\leqslant\mid\alpha\mid+\mid\beta\mid \\ $$$$\mid\beta−\alpha\mid\leqslant\mid\beta\mid+\mid\alpha\mid \\ $$$$\mid\alpha+\left(\beta−\alpha\right)\mid\leqslant\mid\alpha\mid+\mid\beta−\alpha\mid \\ $$$$\mid\beta\mid\leqslant\mid\alpha\mid+\mid\beta−\alpha\mid \\ $$$$\mid\beta\mid−\mid\alpha\mid\leqslant\mid\beta−\alpha\mid\leqslant\mid\beta\mid+\mid\alpha\mid \\ $$$$\mathrm{1}−\mid\alpha\beta\mid\leqslant\mid\mathrm{1}−\alpha\beta\mid\leqslant\mathrm{1}+\mid\alpha\beta\mid \\ $$$$\mid\beta\mid=\mathrm{1}\Rightarrow\beta={e}^{{xi}} ,{x}\in\mathbb{R} \\ $$$$\mathrm{1}−\mid\alpha\mid\leqslant\mid\beta−\alpha\mid\leqslant\mathrm{1}+\mid\alpha\mid \\ $$$$\mathrm{1}−\mid\alpha\mid\leqslant\mid\mathrm{1}−\alpha\beta\mid\leqslant\mathrm{1}+\mid\alpha\mid \\ $$$$\mid\frac{\beta−\alpha}{\mathrm{1}−\alpha\beta}\mid=\frac{\mid\beta−\alpha\mid}{\mid\mathrm{1}−\alpha\beta\mid} \\ $$$$\alpha\beta\neq\mathrm{1} \\ $$$$\alpha\beta\bar {\beta}\neq\bar {\beta} \\ $$$$\alpha\mid\beta\mid^{\mathrm{2}} \neq\bar {\beta} \\ $$$$\alpha\neq\bar {\beta} \\ $$$$\mid\alpha\mid\neq\mid\bar {\beta}\mid=\mid\beta\mid=\mathrm{1} \\ $$$$\mid\alpha\mid\neq\mathrm{1} \\ $$$$\alpha\neq\beta\Rightarrow\mid\beta−\alpha\mid\neq\mathrm{0} \\ $$
Commented by Rasheed Soomro last updated on 23/Jul/15
The answer is α−dependant and it is also not fully free of β. It either depends upon Real(β) or Im(β). However the process of simplification may be as under: ∣ β ∣=1⇒( ∣β∣ )^2 =1⇒β β^− =1 Hence ∣ ((β−α)/(1−αβ)) ∣=∣ ((β−α)/(β β^− −α β)) ∣ (Replacing 1 by β β^− ) =∣ ((β−α)/(β ( β^− −α ))) ∣=∣ (1/β) ∣ . ∣ ((β−α)/(β^− −α)) ∣=(1/(∣ β ∣)) . ∣ ((β −α)/(β^− −α)) ∣ =∣ ((β−α)/(β^− −α)) ∣ ( ∣ β ∣=1 ) =∣ ((β−α)/(β^− −α)) −1+1 ∣=∣ ((β−α−β^− +α)/(β^− −α)) +1∣=∣ ((β−β^− )/(β^− −α))+1∣ Now β−β^− =2i[Re(β)] and β^− =−Re(β)+i[Im(β)^(−) =Re(β)−i[ Im(β) =∣ ((2i [Re(β)])/(Re(β)−i[ Im(β)−α)) +1∣ Here you can express Im(β) in terms of Re(β) or vice versa. As [ Re(β) ]^2 +[ Im(β) ]^2 =1 (∵ ∣β∣=1 ) So Im(β)=±(√(1−[ Re(β) ]^2 )) ∣ ((β−α)/(1−αβ)) ∣ = ∣ ((2i [Re(β)])/(Re(β)−i[ {±(√(1−[ Re(β) ]^2 ))}−α)) +1∣ Or ∣ ((β−α)/(1−αβ)) ∣=∣ ((2i {±(√(1−[Im(β)]^2 )) })/({±(√(1−[Im(β)]^2 )) }−i[ Im(β)−α)) +1∣
$${The}\:{answer}\:{is}\:\alpha−{dependant}\:{and}\:{it}\:{is}\:{also}\:{not}\:{fully}\:{free}\:{of}\:\beta. \\ $$$${It}\:{either}\:{depends}\:{upon}\:{Real}\left(\beta\right)\:{or}\:{Im}\left(\beta\right).\: \\ $$$${However}\:{the}\:{process}\:{of}\:{simplification}\:{may}\:{be}\:{as}\:{under}: \\ $$$$ \\ $$$$\mid\:\beta\:\mid=\mathrm{1}\Rightarrow\left(\:\mid\beta\mid\:\right)^{\mathrm{2}} =\mathrm{1}\Rightarrow\beta\:\overset{−} {\beta}=\mathrm{1} \\ $$$${Hence}\:\mid\:\frac{\beta−\alpha}{\mathrm{1}−\alpha\beta}\:\mid=\mid\:\frac{\beta−\alpha}{\beta\:\overset{−} {\beta}−\alpha\:\beta}\:\mid\:\:\:\:\:\:\:\:\left({Replacing}\:\mathrm{1}\:{by}\:\beta\:\overset{−} {\beta}\:\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mid\:\frac{\beta−\alpha}{\beta\:\left(\:\overset{−} {\beta}−\alpha\:\right)}\:\mid=\mid\:\frac{\mathrm{1}}{\beta}\:\mid\:.\:\mid\:\frac{\beta−\alpha}{\overset{−} {\beta}−\alpha}\:\mid=\frac{\mathrm{1}}{\mid\:\beta\:\mid}\:.\:\mid\:\frac{\beta\:−\alpha}{\overset{−} {\beta}−\alpha}\:\mid \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mid\:\frac{\beta−\alpha}{\overset{−} {\beta}−\alpha}\:\mid\:\:\:\:\:\:\:\:\:\:\:\:\left(\:\mid\:\beta\:\mid=\mathrm{1}\:\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mid\:\frac{\beta−\alpha}{\overset{−} {\beta}−\alpha}\:−\mathrm{1}+\mathrm{1}\:\mid=\mid\:\frac{\beta−\alpha−\overset{−} {\beta}+\alpha}{\overset{−} {\beta}−\alpha}\:+\mathrm{1}\mid=\mid\:\frac{\beta−\overset{−} {\beta}}{\overset{−} {\beta}−\alpha}+\mathrm{1}\mid \\ $$$${Now}\:\beta−\overset{−} {\beta}=\mathrm{2}{i}\left[{Re}\left(\beta\right)\right]\:{and}\:\overset{−} {\beta}=−\overline {{Re}\left(\beta\right)+{i}\left[{Im}\left(\beta\right)}={Re}\left(\beta\right)−{i}\left[\:{Im}\left(\beta\right)\right.\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mid\:\frac{\mathrm{2}{i}\:\left[{Re}\left(\beta\right)\right]}{{Re}\left(\beta\right)−{i}\left[\:{Im}\left(\beta\right)−\alpha\right.}\:+\mathrm{1}\mid \\ $$$$\:\:\:{Here}\:{you}\:{can}\:{express}\:{Im}\left(\beta\right)\:{in}\:{terms}\:{of}\:{Re}\left(\beta\right)\:{or}\:{vice}\:{versa}. \\ $$$$\:\:\:{As}\:\left[\:{Re}\left(\beta\right)\:\right]^{\mathrm{2}} +\left[\:{Im}\left(\beta\right)\:\right]^{\mathrm{2}} =\mathrm{1}\:\:\:\:\:\:\:\left(\because\:\mid\beta\mid=\mathrm{1}\:\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{So}\:\:{Im}\left(\beta\right)=\pm\sqrt{\mathrm{1}−\left[\:{Re}\left(\beta\right)\:\right]^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\:\frac{\beta−\alpha}{\mathrm{1}−\alpha\beta}\:\mid\:=\:\mid\:\frac{\mathrm{2}{i}\:\left[{Re}\left(\beta\right)\right]}{{Re}\left(\beta\right)−{i}\left[\:\left\{\pm\sqrt{\mathrm{1}−\left[\:{Re}\left(\beta\right)\:\right]^{\mathrm{2}} }\right\}−\alpha\right.}\:+\mathrm{1}\mid \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{Or} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\:\frac{\beta−\alpha}{\mathrm{1}−\alpha\beta}\:\mid=\mid\:\frac{\mathrm{2}{i}\:\left\{\pm\sqrt{\mathrm{1}−\left[{Im}\left(\beta\right)\right]^{\mathrm{2}} \:}\:\right\}}{\left\{\pm\sqrt{\mathrm{1}−\left[{Im}\left(\beta\right)\right]^{\mathrm{2}} \:}\:\right\}−{i}\left[\:{Im}\left(\beta\right)−\alpha\right.}\:+\mathrm{1}\mid \\ $$$$ \\ $$
Answered by prakash jain last updated on 23/Jul/15
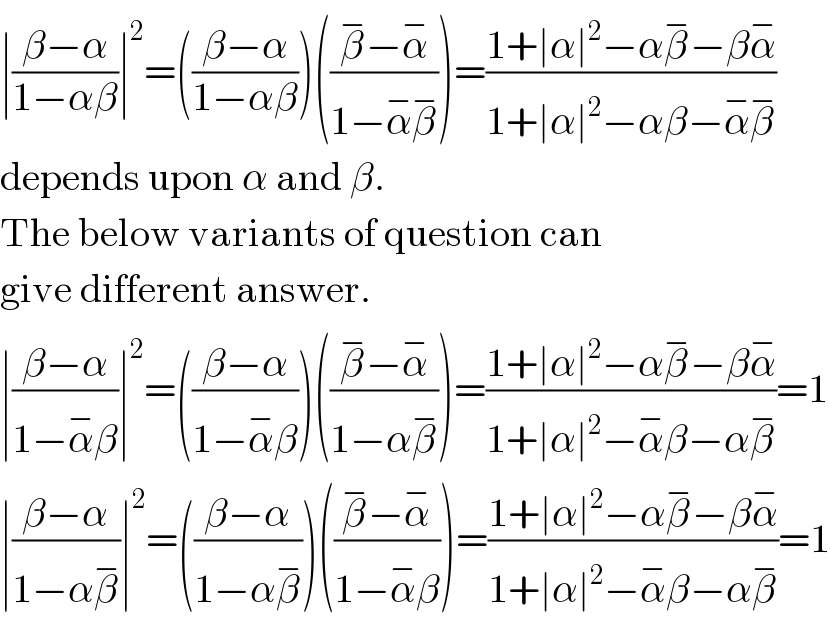
∣((β−α)/(1−αβ))∣^2 =(((β−α)/(1−αβ)))(((β^− −α^− )/(1−α^− β^− )))=((1+∣α∣^2 −αβ^− −βα^− )/(1+∣α∣^2 −αβ−α^− β^− )) depends upon α and β. The below variants of question can give different answer. ∣((β−α)/(1−α^− β))∣^2 =(((β−α)/(1−α^− β)))(((β^− −α^− )/(1−αβ^− )))=((1+∣α∣^2 −αβ^− −βα^− )/(1+∣α∣^2 −α^− β−αβ^− ))=1 ∣((β−α)/(1−αβ^− ))∣^2 =(((β−α)/(1−αβ^− )))(((β^− −α^− )/(1−α^− β)))=((1+∣α∣^2 −αβ^− −βα^− )/(1+∣α∣^2 −α^− β−αβ^− ))=1
$$\mid\frac{\beta−\alpha}{\mathrm{1}−\alpha\beta}\mid^{\mathrm{2}} =\left(\frac{\beta−\alpha}{\mathrm{1}−\alpha\beta}\right)\left(\frac{\overset{−} {\beta}−\overset{−} {\alpha}}{\mathrm{1}−\overset{−} {\alpha}\overset{−} {\beta}}\right)=\frac{\mathrm{1}+\mid\alpha\mid^{\mathrm{2}} −\alpha\overset{−} {\beta}−\beta\overset{−} {\alpha}}{\mathrm{1}+\mid\alpha\mid^{\mathrm{2}} −\alpha\beta−\overset{−} {\alpha}\overset{−} {\beta}} \\ $$$$\mathrm{depends}\:\mathrm{upon}\:\alpha\:\mathrm{and}\:\beta. \\ $$$$\mathrm{The}\:\mathrm{below}\:\mathrm{variants}\:\mathrm{of}\:\mathrm{question}\:\mathrm{can} \\ $$$$\mathrm{give}\:\mathrm{different}\:\mathrm{answer}. \\ $$$$\mid\frac{\beta−\alpha}{\mathrm{1}−\overset{−} {\alpha}\beta}\mid^{\mathrm{2}} =\left(\frac{\beta−\alpha}{\mathrm{1}−\overset{−} {\alpha}\beta}\right)\left(\frac{\overset{−} {\beta}−\overset{−} {\alpha}}{\mathrm{1}−\alpha\overset{−} {\beta}}\right)=\frac{\mathrm{1}+\mid\alpha\mid^{\mathrm{2}} −\alpha\overset{−} {\beta}−\beta\overset{−} {\alpha}}{\mathrm{1}+\mid\alpha\mid^{\mathrm{2}} −\overset{−} {\alpha}\beta−\alpha\overset{−} {\beta}}=\mathrm{1} \\ $$$$\mid\frac{\beta−\alpha}{\mathrm{1}−\alpha\overset{−} {\beta}}\mid^{\mathrm{2}} =\left(\frac{\beta−\alpha}{\mathrm{1}−\alpha\overset{−} {\beta}}\right)\left(\frac{\overset{−} {\beta}−\overset{−} {\alpha}}{\mathrm{1}−\overset{−} {\alpha}\beta}\right)=\frac{\mathrm{1}+\mid\alpha\mid^{\mathrm{2}} −\alpha\overset{−} {\beta}−\beta\overset{−} {\alpha}}{\mathrm{1}+\mid\alpha\mid^{\mathrm{2}} −\overset{−} {\alpha}\beta−\alpha\overset{−} {\beta}}=\mathrm{1} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *