Question Number 138766 by nadovic last updated on 18/Apr/21
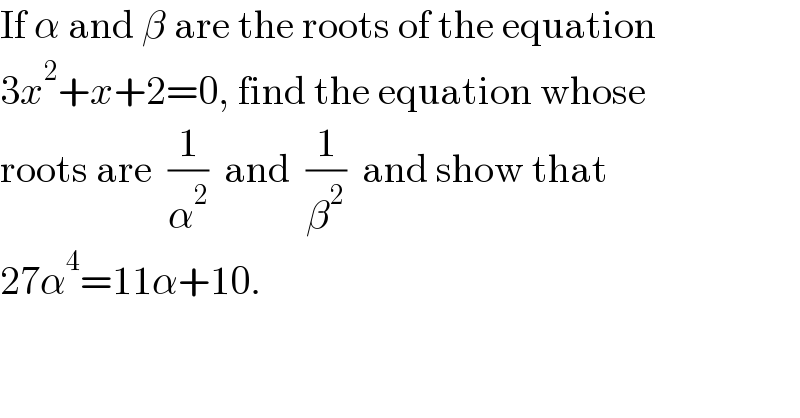
$$\mathrm{If}\:\alpha\:\mathrm{and}\:\beta\:\mathrm{are}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} +{x}+\mathrm{2}=\mathrm{0},\:\mathrm{find}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{whose} \\ $$$$\mathrm{roots}\:\mathrm{are}\:\:\frac{\mathrm{1}}{\alpha^{\mathrm{2}} }\:\:\mathrm{and}\:\:\frac{\mathrm{1}}{\beta^{\mathrm{2}} }\:\:\mathrm{and}\:\mathrm{show}\:\mathrm{that} \\ $$$$\mathrm{27}\alpha^{\mathrm{4}} =\mathrm{11}\alpha+\mathrm{10}. \\ $$
Commented by MJS_new last updated on 18/Apr/21
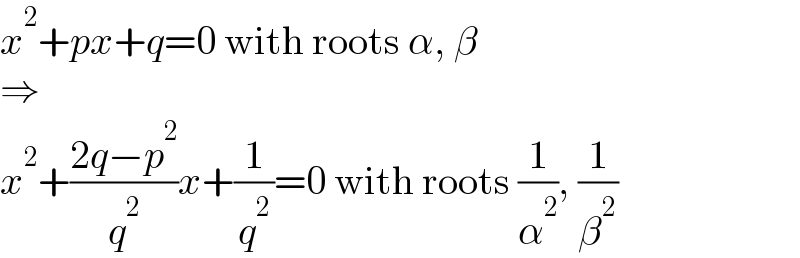
$${x}^{\mathrm{2}} +{px}+{q}=\mathrm{0}\:\mathrm{with}\:\mathrm{roots}\:\alpha,\:\beta \\ $$$$\Rightarrow \\ $$$${x}^{\mathrm{2}} +\frac{\mathrm{2}{q}−{p}^{\mathrm{2}} }{{q}^{\mathrm{2}} }{x}+\frac{\mathrm{1}}{{q}^{\mathrm{2}} }=\mathrm{0}\:\mathrm{with}\:\mathrm{roots}\:\frac{\mathrm{1}}{\alpha^{\mathrm{2}} },\:\frac{\mathrm{1}}{\beta^{\mathrm{2}} } \\ $$
Answered by bramlexs22 last updated on 18/Apr/21
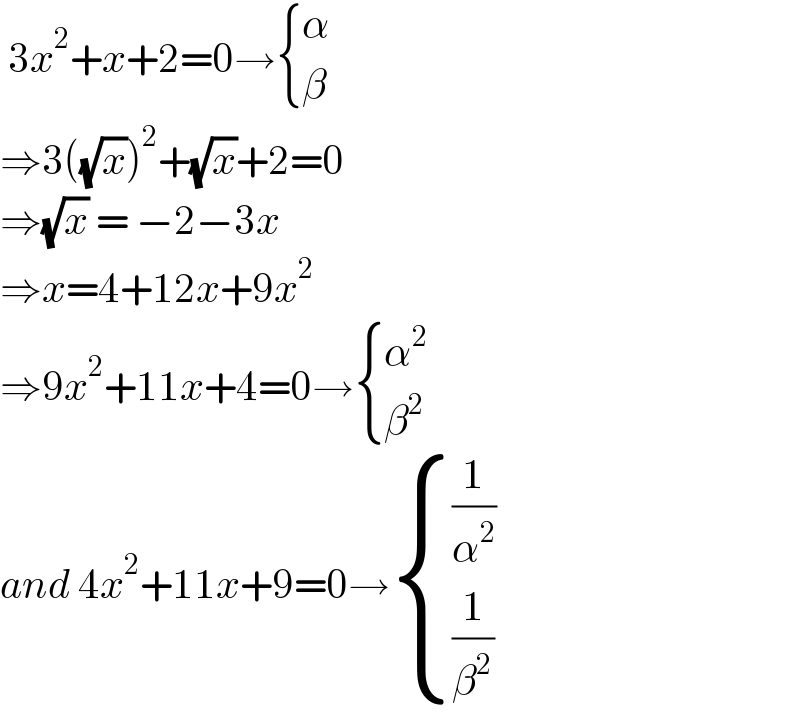
$$\:\mathrm{3}{x}^{\mathrm{2}} +{x}+\mathrm{2}=\mathrm{0}\rightarrow\begin{cases}{\alpha}\\{\beta}\end{cases} \\ $$$$\Rightarrow\mathrm{3}\left(\sqrt{{x}}\right)^{\mathrm{2}} +\sqrt{{x}}+\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\sqrt{{x}}\:=\:−\mathrm{2}−\mathrm{3}{x}\: \\ $$$$\Rightarrow{x}=\mathrm{4}+\mathrm{12}{x}+\mathrm{9}{x}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{9}{x}^{\mathrm{2}} +\mathrm{11}{x}+\mathrm{4}=\mathrm{0}\rightarrow\begin{cases}{\alpha^{\mathrm{2}} }\\{\beta^{\mathrm{2}} }\end{cases} \\ $$$${and}\:\mathrm{4}{x}^{\mathrm{2}} +\mathrm{11}{x}+\mathrm{9}=\mathrm{0}\rightarrow\begin{cases}{\frac{\mathrm{1}}{\alpha^{\mathrm{2}} }}\\{\frac{\mathrm{1}}{\beta^{\mathrm{2}} }}\end{cases} \\ $$
Commented by Rasheed.Sindhi last updated on 18/Apr/21
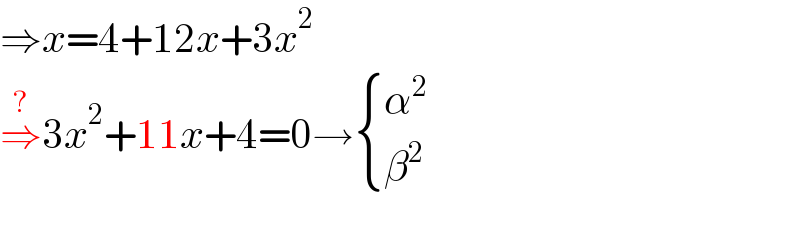
$$\Rightarrow{x}=\mathrm{4}+\mathrm{12}{x}+\mathrm{3}{x}^{\mathrm{2}} \\ $$$$\overset{?} {\Rightarrow}\mathrm{3}{x}^{\mathrm{2}} +\mathrm{11}{x}+\mathrm{4}=\mathrm{0}\rightarrow\begin{cases}{\alpha^{\mathrm{2}} }\\{\beta^{\mathrm{2}} }\end{cases} \\ $$$$ \\ $$
Commented by bramlexs22 last updated on 18/Apr/21

$${typo} \\ $$
Answered by Rasheed.Sindhi last updated on 18/Apr/21
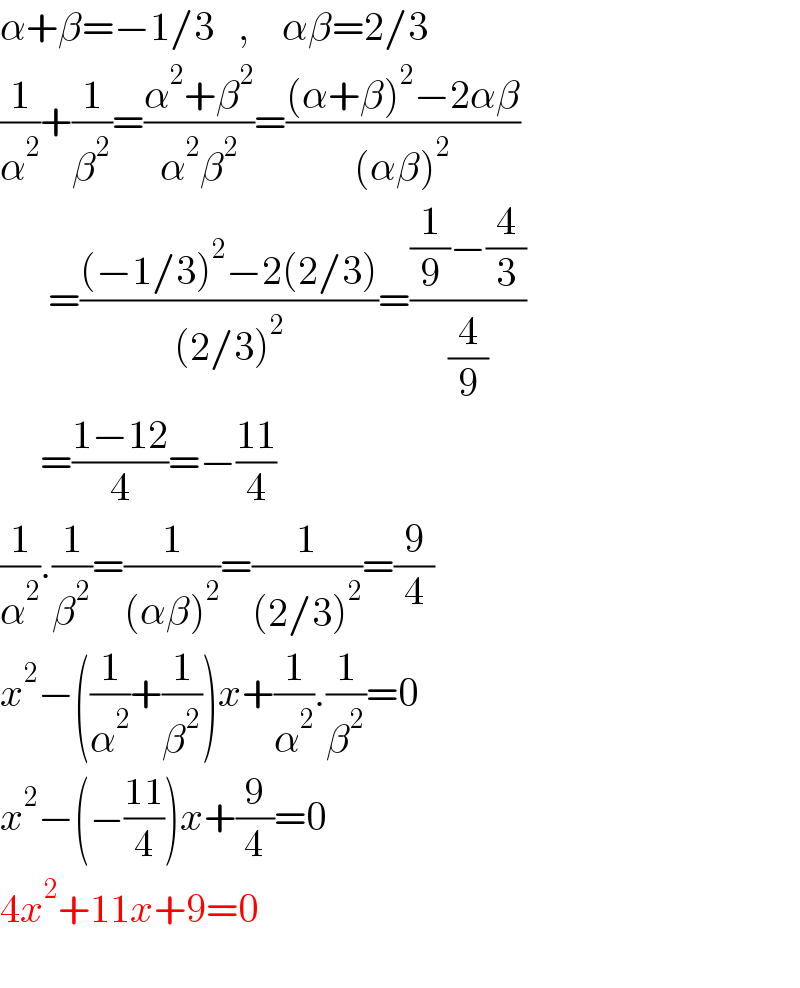
$$\alpha+\beta=−\mathrm{1}/\mathrm{3}\:\:\:,\:\:\:\:\alpha\beta=\mathrm{2}/\mathrm{3} \\ $$$$\frac{\mathrm{1}}{\alpha^{\mathrm{2}} }+\frac{\mathrm{1}}{\beta^{\mathrm{2}} }=\frac{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }{\alpha^{\mathrm{2}} \beta^{\mathrm{2}} }=\frac{\left(\alpha+\beta\right)^{\mathrm{2}} −\mathrm{2}\alpha\beta}{\left(\alpha\beta\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:=\frac{\left(−\mathrm{1}/\mathrm{3}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{2}/\mathrm{3}\right)}{\left(\mathrm{2}/\mathrm{3}\right)^{\mathrm{2}} }=\frac{\frac{\mathrm{1}}{\mathrm{9}}−\frac{\mathrm{4}}{\mathrm{3}}}{\frac{\mathrm{4}}{\mathrm{9}}} \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}−\mathrm{12}}{\mathrm{4}}=−\frac{\mathrm{11}}{\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{\alpha^{\mathrm{2}} }.\frac{\mathrm{1}}{\beta^{\mathrm{2}} }=\frac{\mathrm{1}}{\left(\alpha\beta\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\left(\mathrm{2}/\mathrm{3}\right)^{\mathrm{2}} }=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$${x}^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\alpha^{\mathrm{2}} }+\frac{\mathrm{1}}{\beta^{\mathrm{2}} }\right){x}+\frac{\mathrm{1}}{\alpha^{\mathrm{2}} }.\frac{\mathrm{1}}{\beta^{\mathrm{2}} }=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\left(−\frac{\mathrm{11}}{\mathrm{4}}\right){x}+\frac{\mathrm{9}}{\mathrm{4}}=\mathrm{0} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} +\mathrm{11}{x}+\mathrm{9}=\mathrm{0} \\ $$$$ \\ $$
Answered by physicstutes last updated on 18/Apr/21
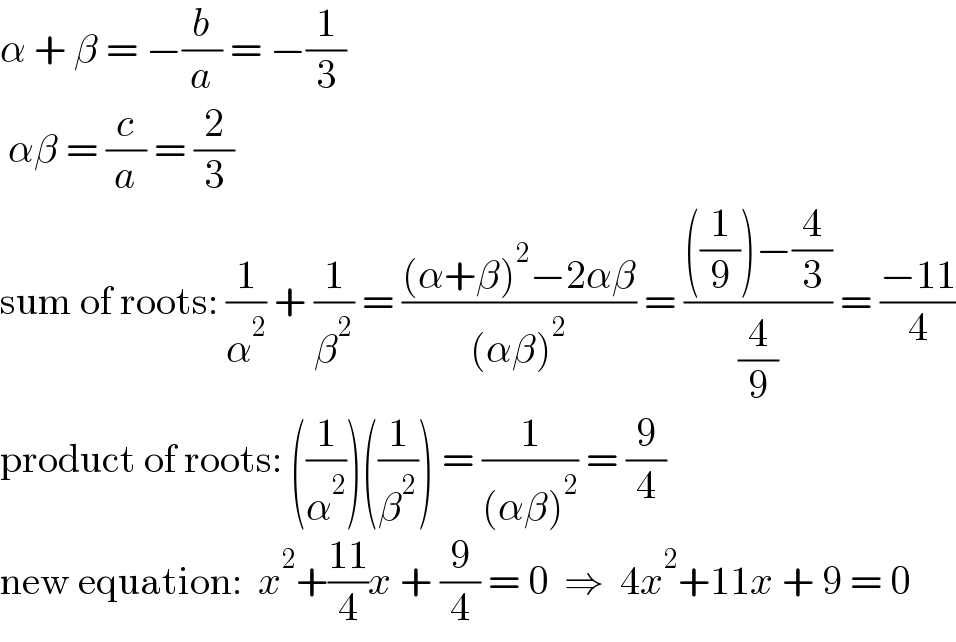
$$\alpha\:+\:\beta\:=\:−\frac{{b}}{{a}}\:=\:−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\:\alpha\beta\:=\:\frac{{c}}{{a}}\:=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\mathrm{sum}\:\mathrm{of}\:\mathrm{roots}:\:\frac{\mathrm{1}}{\alpha^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\beta^{\mathrm{2}} }\:=\:\frac{\left(\alpha+\beta\right)^{\mathrm{2}} −\mathrm{2}\alpha\beta}{\left(\alpha\beta\right)^{\mathrm{2}} }\:=\:\frac{\left(\frac{\mathrm{1}}{\mathrm{9}}\right)−\frac{\mathrm{4}}{\mathrm{3}}}{\frac{\mathrm{4}}{\mathrm{9}}}\:=\:\frac{−\mathrm{11}}{\mathrm{4}} \\ $$$$\mathrm{product}\:\mathrm{of}\:\mathrm{roots}:\:\left(\frac{\mathrm{1}}{\alpha^{\mathrm{2}} }\right)\left(\frac{\mathrm{1}}{\beta^{\mathrm{2}} }\right)\:=\:\frac{\mathrm{1}}{\left(\alpha\beta\right)^{\mathrm{2}} }\:=\:\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\mathrm{new}\:\mathrm{equation}:\:\:{x}^{\mathrm{2}} +\frac{\mathrm{11}}{\mathrm{4}}{x}\:+\:\frac{\mathrm{9}}{\mathrm{4}}\:=\:\mathrm{0}\:\:\Rightarrow\:\:\mathrm{4}{x}^{\mathrm{2}} +\mathrm{11}{x}\:+\:\mathrm{9}\:=\:\mathrm{0} \\ $$
