Question Number 6148 by saiful last updated on 16/Jun/16

$${if}\:\alpha,\beta\:{and}\gamma\:{is}\:{corner}\:{in}\:\Delta{abc}.\:{indication}\:{that}\:{cos}\left(\beta+\gamma\right)=−{cos}\alpha \\ $$
Answered by Rasheed Soomro last updated on 16/Jun/16
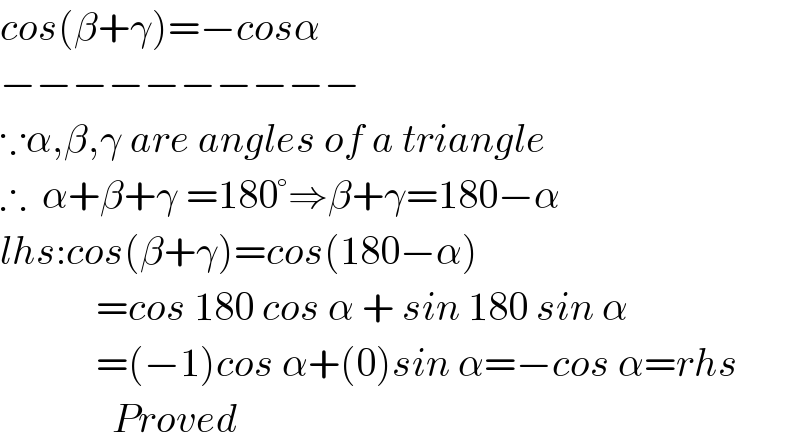
$${cos}\left(\beta+\gamma\right)=−{cos}\alpha \\ $$$$−−−−−−−−−− \\ $$$$\because\alpha,\beta,\gamma\:{are}\:{angles}\:{of}\:{a}\:{triangle} \\ $$$$\therefore\:\:\alpha+\beta+\gamma\:=\mathrm{180}°\Rightarrow\beta+\gamma=\mathrm{180}−\alpha \\ $$$${lhs}:{cos}\left(\beta+\gamma\right)={cos}\left(\mathrm{180}−\alpha\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:={cos}\:\mathrm{180}\:{cos}\:\alpha\:+\:{sin}\:\mathrm{180}\:{sin}\:\alpha \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\left(−\mathrm{1}\right){cos}\:\alpha+\left(\mathrm{0}\right){sin}\:\alpha=−{cos}\:\alpha={rhs} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{Proved} \\ $$
