If-asin-1-x-bcos-1-x-c-then-the-value-of-asin-1-x-bcos-1-x-whenever-exists-is-equal-to-

Question Number 131296 by EDWIN88 last updated on 03/Feb/21

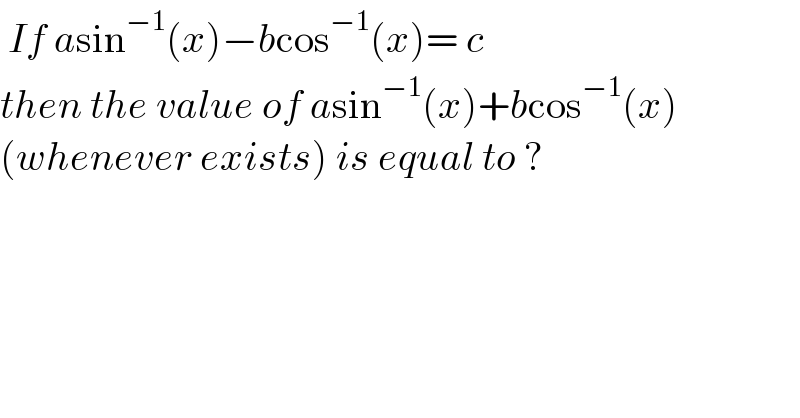
I f a \sin^{- 1} (x) - b \cos^{- 1} (x) = c

t h e n t h e v a l u e o f a \sin^{- 1} (x) + b \cos^{- 1} (x)

(w h e n e v e r e x i s t s) i s e q u a l t o ?

Answered by liberty last updated on 03/Feb/21

We have \sin^{- 1} (x) + \cos^{- 1} (x) = \frac{π}{2}

then {bsin}^{- 1} (x) + {bcos}^{- 1} (x) = \frac{b π}{2} \dots (i)

{asin}^{- 1} (x) - {bcos}^{- 1} (x) = c \dots (ii)

∴ on adding (i) and (ii) we get

\sin^{- 1} (x) = \frac{\frac{b π}{2} + c}{a + b} and \cos^{- 1} (x) = \frac{\frac{a π}{2} - c}{a + b}

Therefore {asin}^{- 1} (x) + {bcos}^{- 1} (x) = \frac{π ab + c (a - b)}{a + b}

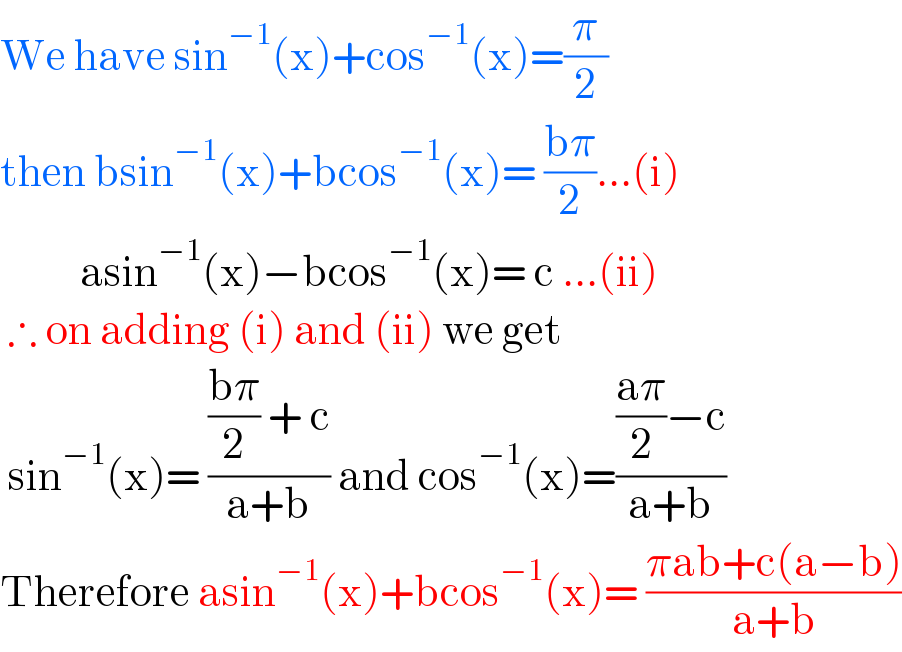
Commented by EDWIN88 last updated on 03/Feb/21

sehr interessante Erklrung Sir

Answered by mr W last updated on 03/Feb/21

t = \sin^{- 1} x

\frac{π}{2} - t = \cos^{- 1} x

a \sin^{- 1} (x) - b \cos^{- 1} (x) = c

\Rightarrow a t - b (\frac{π}{2} - t) = c

\Rightarrow (a + b) t = c + \frac{b π}{2}

\Rightarrow t = \frac{1}{a + b} (c + \frac{b π}{2})

a \sin^{- 1} (x) + b \cos^{- 1} (x)

= a t + b (\frac{π}{2} - t)

= (a - b) t + \frac{b π}{2}

= \frac{a - b}{a + b} (c + \frac{b π}{2}) + \frac{b π}{2}

= \frac{(a - b) c + a b π}{a + b}

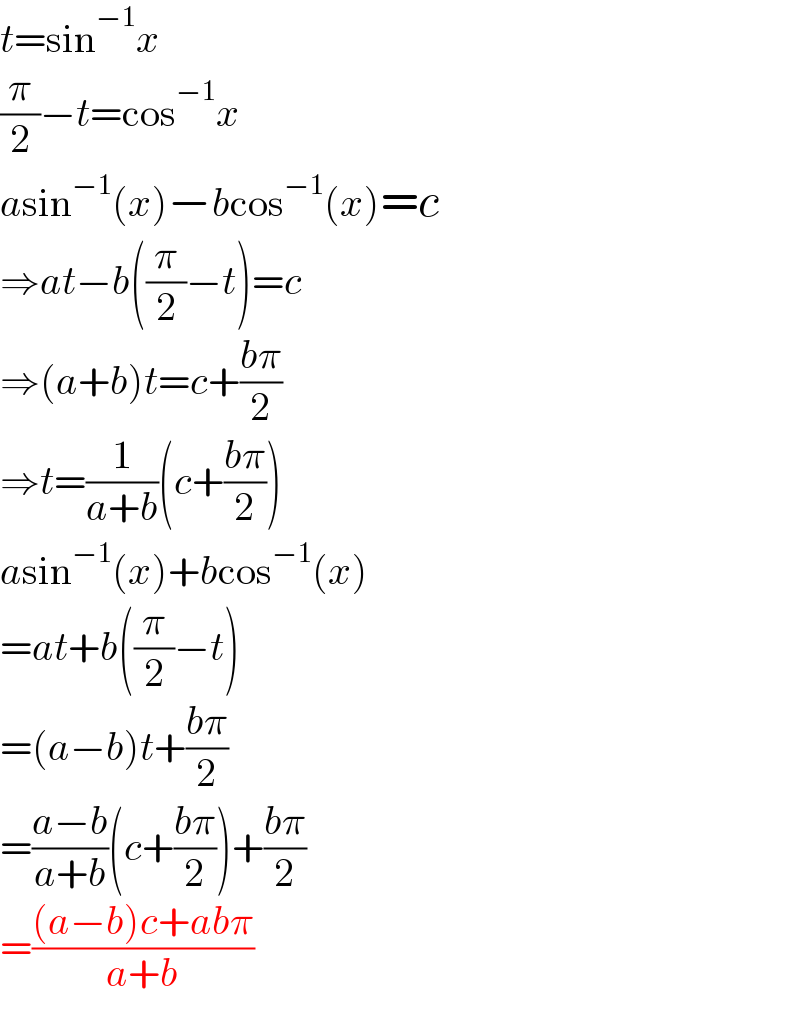
Commented by EDWIN88 last updated on 03/Feb/21

n i c e

Facebook Tweet Pin