Question Number 10948 by rish@bh last updated on 03/Mar/17
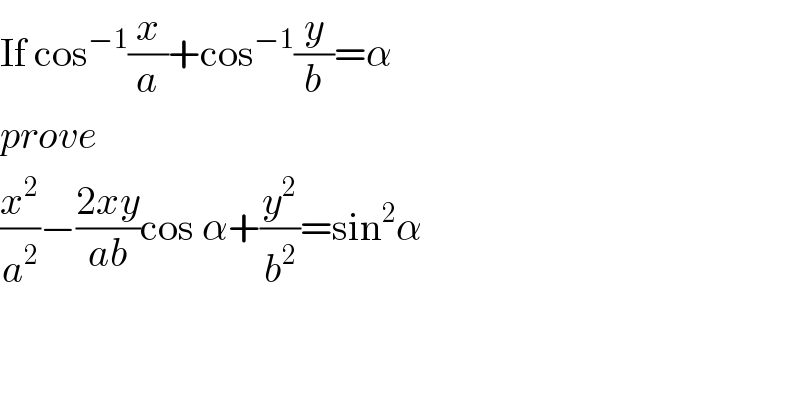
$$\mathrm{If}\:\mathrm{cos}^{−\mathrm{1}} \frac{{x}}{{a}}+\mathrm{cos}^{−\mathrm{1}} \frac{{y}}{{b}}=\alpha \\ $$$${prove}\: \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\frac{\mathrm{2}{xy}}{{ab}}\mathrm{cos}\:\alpha+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{sin}^{\mathrm{2}} \alpha \\ $$
Answered by ajfour last updated on 03/Mar/17

$$ \\ $$$$ \\ $$$${let}\:\theta+\emptyset=\alpha \\ $$$$\mathrm{cos}\:\left(\theta+\emptyset\right)=\mathrm{cos}\:\alpha \\ $$$$\mathrm{cos}\:\theta\mathrm{cos}\:\emptyset−\mathrm{sin}\:\theta\mathrm{sin}\:\emptyset=\mathrm{cos}\:\alpha \\ $$$$\left(\frac{{x}}{{a}}\right)\left(\frac{{y}}{{b}}\right)−\frac{\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }}{{a}}.\frac{\sqrt{{b}^{\mathrm{2}} −{y}^{\mathrm{2}} }}{{b}}=\mathrm{cos}\:\alpha \\ $$$$\left(\frac{{xy}}{{ab}}−\mathrm{cos}\:\alpha\right)^{\mathrm{2}} =\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right) \\ $$$$−\frac{\mathrm{2}{xy}\mathrm{cos}\:\alpha}{{ab}}+\mathrm{cos}\:^{\mathrm{2}} \alpha\:=\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\frac{\mathrm{2}{xy}\mathrm{cos}\:\alpha}{{ab}}+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:=\mathrm{sin}\:^{\mathrm{2}} \alpha\:. \\ $$
Commented by rish@bh last updated on 03/Mar/17

$$\mathrm{Thank}\:\mathrm{you} \\ $$
