Question Number 73665 by aliesam last updated on 14/Nov/19
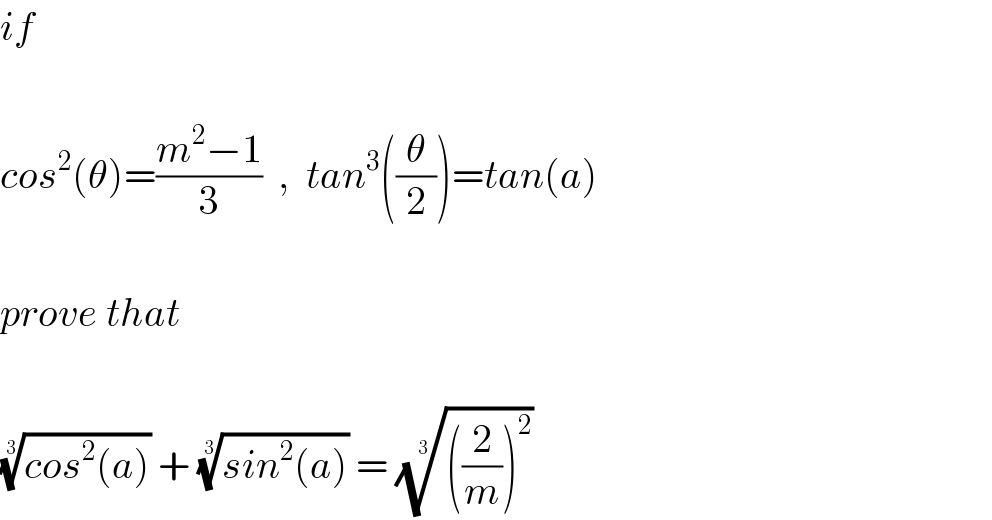
$${if} \\ $$$$ \\ $$$${cos}^{\mathrm{2}} \left(\theta\right)=\frac{{m}^{\mathrm{2}} −\mathrm{1}}{\mathrm{3}}\:\:,\:\:{tan}^{\mathrm{3}} \left(\frac{\theta}{\mathrm{2}}\right)={tan}\left({a}\right) \\ $$$$ \\ $$$${prove}\:{that} \\ $$$$ \\ $$$$\sqrt[{\mathrm{3}}]{{cos}^{\mathrm{2}} \left({a}\right)}\:+\:\sqrt[{\mathrm{3}}]{{sin}^{\mathrm{2}} \left({a}\right)}\:=\:\sqrt[{\mathrm{3}}]{\left(\frac{\mathrm{2}}{{m}}\right)^{\mathrm{2}} } \\ $$
Answered by Tanmay chaudhury last updated on 14/Nov/19
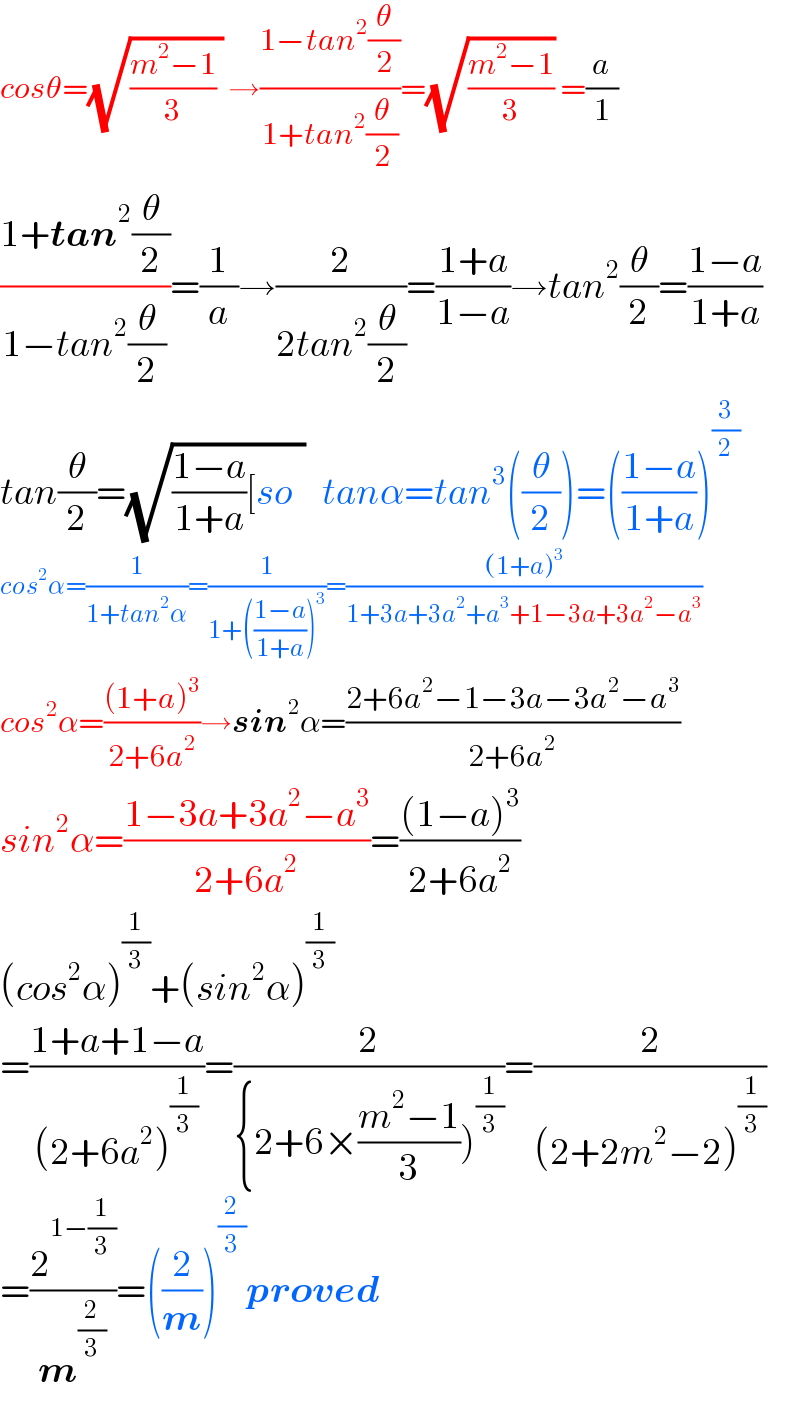
$${cos}\theta=\sqrt{\frac{{m}^{\mathrm{2}} −\mathrm{1}}{\mathrm{3}}\:}\:\rightarrow\frac{\mathrm{1}−{tan}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}}{\mathrm{1}+{tan}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}}=\sqrt{\frac{{m}^{\mathrm{2}} −\mathrm{1}}{\mathrm{3}}}\:=\frac{{a}}{\mathrm{1}} \\ $$$$\frac{\mathrm{1}+\boldsymbol{{tan}}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}}{\mathrm{1}−{tan}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}}=\frac{\mathrm{1}}{{a}}\rightarrow\frac{\mathrm{2}}{\mathrm{2}{tan}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}}=\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}\rightarrow{tan}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}=\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}} \\ $$$${tan}\frac{\theta}{\mathrm{2}}=\sqrt{\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}\left[{so}\:\:\right.}\:\:\:{tan}\alpha={tan}^{\mathrm{3}} \left(\frac{\theta}{\mathrm{2}}\right)=\left(\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$${cos}^{\mathrm{2}} \alpha=\frac{\mathrm{1}}{\mathrm{1}+{tan}^{\mathrm{2}} \alpha}=\frac{\mathrm{1}}{\mathrm{1}+\left(\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}\right)^{\mathrm{3}} }=\frac{\left(\mathrm{1}+{a}\right)^{\mathrm{3}} }{\mathrm{1}+\mathrm{3}{a}+\mathrm{3}{a}^{\mathrm{2}} +{a}^{\mathrm{3}} +\mathrm{1}−\mathrm{3}{a}+\mathrm{3}{a}^{\mathrm{2}} −{a}^{\mathrm{3}} } \\ $$$${cos}^{\mathrm{2}} \alpha=\frac{\left(\mathrm{1}+{a}\right)^{\mathrm{3}} }{\mathrm{2}+\mathrm{6}{a}^{\mathrm{2}} }\rightarrow\boldsymbol{{sin}}^{\mathrm{2}} \alpha=\frac{\mathrm{2}+\mathrm{6}{a}^{\mathrm{2}} −\mathrm{1}−\mathrm{3}{a}−\mathrm{3}{a}^{\mathrm{2}} −{a}^{\mathrm{3}} }{\mathrm{2}+\mathrm{6}{a}^{\mathrm{2}} } \\ $$$${sin}^{\mathrm{2}} \alpha=\frac{\mathrm{1}−\mathrm{3}{a}+\mathrm{3}{a}^{\mathrm{2}} −{a}^{\mathrm{3}} }{\mathrm{2}+\mathrm{6}{a}^{\mathrm{2}} }=\frac{\left(\mathrm{1}−{a}\right)^{\mathrm{3}} }{\mathrm{2}+\mathrm{6}{a}^{\mathrm{2}} } \\ $$$$\left({cos}^{\mathrm{2}} \alpha\right)^{\frac{\mathrm{1}}{\mathrm{3}}} +\left({sin}^{\mathrm{2}} \alpha\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$=\frac{\mathrm{1}+{a}+\mathrm{1}−{a}}{\left(\mathrm{2}+\mathrm{6}{a}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} }=\frac{\mathrm{2}}{\left\{\mathrm{2}+\mathrm{6}×\frac{{m}^{\mathrm{2}} −\mathrm{1}}{\mathrm{3}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }=\frac{\mathrm{2}}{\left(\mathrm{2}+\mathrm{2}{m}^{\mathrm{2}} −\mathrm{2}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} } \\ $$$$=\frac{\mathrm{2}^{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}} }{\boldsymbol{{m}}^{\frac{\mathrm{2}}{\mathrm{3}}} }=\left(\frac{\mathrm{2}}{\boldsymbol{{m}}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \boldsymbol{{proved}} \\ $$
