if-cos-4-x-cos-2-y-sin-4-x-sin-2-y-1-then-find-cos-4-y-cos-2-x-sin-4-y-sin-2-x-

Question Number 143348 by gsk2684 last updated on 13/Jun/21

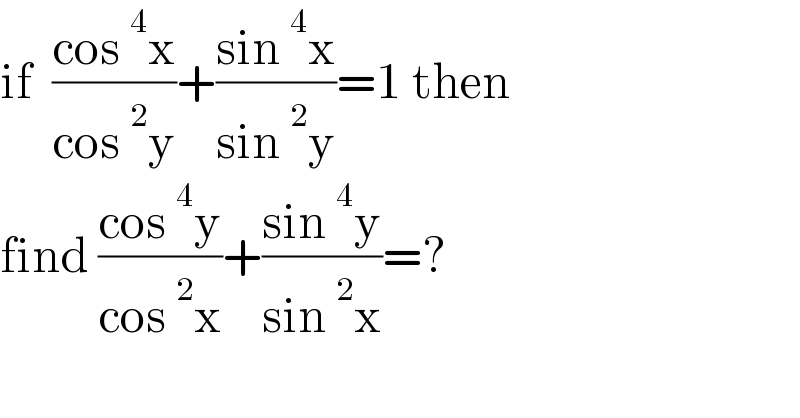
$$\mathrm{if}\:\:\frac{\mathrm{cos}\:^{\mathrm{4}} \mathrm{x}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{y}}+\frac{\mathrm{sin}\:^{\mathrm{4}} \mathrm{x}}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{y}}=\mathrm{1}\:\mathrm{then}\: \\ $$$$\mathrm{find}\:\frac{\mathrm{cos}\:^{\mathrm{4}} \mathrm{y}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}}+\frac{\mathrm{sin}\:^{\mathrm{4}} \mathrm{y}}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}=? \\ $$

Answered by som(math1967) last updated on 13/Jun/21

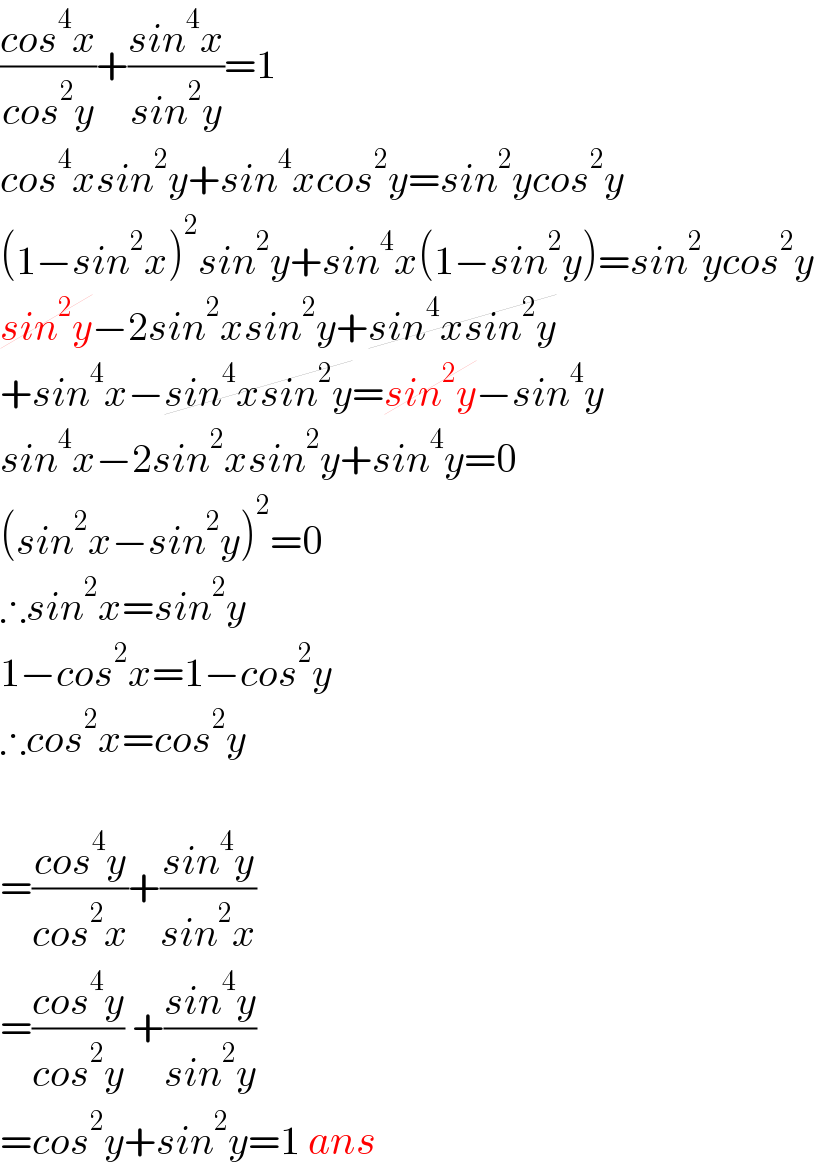
((cos^4 x)/(cos^2 y))+((sin^4 x)/(sin^2 y))=1 cos^4 xsin^2 y+sin^4 xcos^2 y=sin^2 ycos^2 y (1−sin^2 x)^2 sin^2 y+sin^4 x(1−sin^2 y)=sin^2 ycos^2 y sin^2 y−2sin^2 xsin^2 y+sin^4 xsin^2 y +sin^4 x−sin^4 xsin^2 y=sin^2 y−sin^4 y sin^4 x−2sin^2 xsin^2 y+sin^4 y=0 (sin^2 x−sin^2 y)^2 =0 ∴sin^2 x=sin^2 y 1−cos^2 x=1−cos^2 y ∴cos^2 x=cos^2 y =((cos^4 y)/(cos^2 x))+((sin^4 y)/(sin^2 x)) =((cos^4 y)/(cos^2 y)) +((sin^4 y)/(sin^2 y)) =cos^2 y+sin^2 y=1 ans

$$\frac{{cos}^{\mathrm{4}} {x}}{{cos}^{\mathrm{2}} {y}}+\frac{{sin}^{\mathrm{4}} {x}}{{sin}^{\mathrm{2}} {y}}=\mathrm{1} \\ $$$${cos}^{\mathrm{4}} {xsin}^{\mathrm{2}} {y}+{sin}^{\mathrm{4}} {xcos}^{\mathrm{2}} {y}={sin}^{\mathrm{2}} {ycos}^{\mathrm{2}} {y} \\ $$$$\left(\mathrm{1}−{sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} {sin}^{\mathrm{2}} {y}+{sin}^{\mathrm{4}} {x}\left(\mathrm{1}−{sin}^{\mathrm{2}} {y}\right)={sin}^{\mathrm{2}} {ycos}^{\mathrm{2}} {y} \\ $$$$\cancel{{sin}^{\mathrm{2}} {y}}−\mathrm{2}{sin}^{\mathrm{2}} {xsin}^{\mathrm{2}} {y}+\cancel{{sin}^{\mathrm{4}} {xsin}^{\mathrm{2}} {y}} \\ $$$$+{sin}^{\mathrm{4}} {x}−\cancel{{sin}^{\mathrm{4}} {xsin}^{\mathrm{2}} {y}}=\cancel{{sin}^{\mathrm{2}} {y}}−{sin}^{\mathrm{4}} {y} \\ $$$${sin}^{\mathrm{4}} {x}−\mathrm{2}{sin}^{\mathrm{2}} {xsin}^{\mathrm{2}} {y}+{sin}^{\mathrm{4}} {y}=\mathrm{0} \\ $$$$\left({sin}^{\mathrm{2}} {x}−{sin}^{\mathrm{2}} {y}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\therefore{sin}^{\mathrm{2}} {x}={sin}^{\mathrm{2}} {y} \\ $$$$\mathrm{1}−{cos}^{\mathrm{2}} {x}=\mathrm{1}−{cos}^{\mathrm{2}} {y} \\ $$$$\therefore{cos}^{\mathrm{2}} {x}={cos}^{\mathrm{2}} {y} \\ $$$$ \\ $$$$=\frac{{cos}^{\mathrm{4}} {y}}{{cos}^{\mathrm{2}} {x}}+\frac{{sin}^{\mathrm{4}} {y}}{{sin}^{\mathrm{2}} {x}} \\ $$$$=\frac{{cos}^{\mathrm{4}} {y}}{{cos}^{\mathrm{2}} {y}}\:+\frac{{sin}^{\mathrm{4}} {y}}{{sin}^{\mathrm{2}} {y}} \\ $$$$={cos}^{\mathrm{2}} {y}+{sin}^{\mathrm{2}} {y}=\mathrm{1}\:{ans} \\ $$

Commented by gsk2684 last updated on 13/Jun/21

$$\mathscr{T}\mathrm{hank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

if-cos-4-x-cos-2-y-sin-4-x-sin-2-y-1-then-find-cos-4-y-cos-2-x-sin-4-y-sin-2-x-

Leave a Reply Cancel reply