Menu Close

If-Cos-x-cos-y-x-y-cos-then-prove-that-tan-2-x-y-x-y-tan-2-

Tinku Tara 0 Comments
Pin




Question Number 71918 by lalitchand last updated on 22/Oct/19
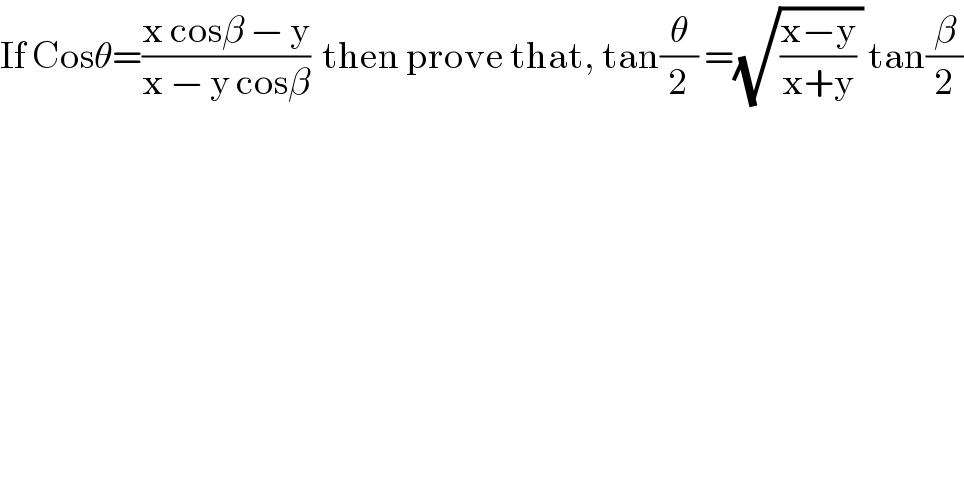
If Cosθ=((x cosβ − y)/(x − y cosβ)) then prove that, tan(θ/2) =(√(((x−y)/(x+y)) )) tan(β/2)
$$\mathrm{If}\:\mathrm{Cos}\theta=\frac{\mathrm{x}\:\mathrm{cos}\beta\:−\:\mathrm{y}}{\mathrm{x}\:−\:\mathrm{y}\:\mathrm{cos}\beta}\:\:\mathrm{then}\:\mathrm{prove}\:\mathrm{that},\:\mathrm{tan}\frac{\theta}{\mathrm{2}}\:=\sqrt{\frac{\mathrm{x}−\mathrm{y}}{\mathrm{x}+\mathrm{y}}\:}\:\mathrm{tan}\frac{\beta}{\mathrm{2}} \\ $$
Commented by Prithwish sen last updated on 22/Oct/19
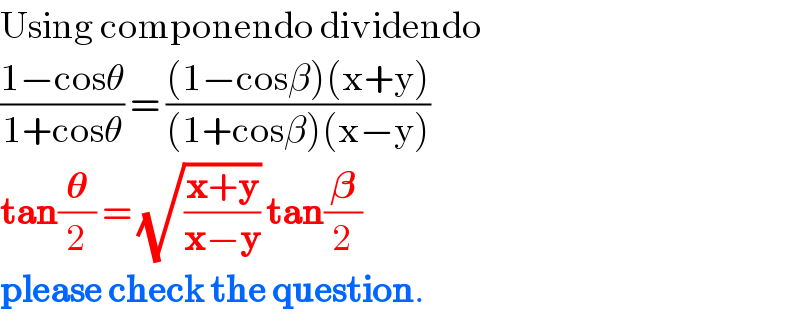
Using componendo dividendo ((1−cosθ)/(1+cosθ)) = (((1−cosβ)(x+y))/((1+cosβ)(x−y))) tan(𝛉/2) = (√((x+y)/(x−y))) tan(𝛃/2) please check the question.
$$\mathrm{Using}\:\mathrm{componendo}\:\mathrm{dividendo} \\ $$$$\frac{\mathrm{1}−\mathrm{cos}\theta}{\mathrm{1}+\mathrm{cos}\theta}\:=\:\frac{\left(\mathrm{1}−\mathrm{cos}\beta\right)\left(\mathrm{x}+\mathrm{y}\right)}{\left(\mathrm{1}+\mathrm{cos}\beta\right)\left(\mathrm{x}−\mathrm{y}\right)} \\ $$$$\boldsymbol{\mathrm{tan}}\frac{\boldsymbol{\theta}}{\mathrm{2}}\:=\:\sqrt{\frac{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}}{\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{y}}}}\:\boldsymbol{\mathrm{tan}}\frac{\boldsymbol{\beta}}{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{question}}. \\ $$
Commented by lalitchand last updated on 22/Oct/19
Is there mistake sir??
$$\mathrm{Is}\:\mathrm{there}\:\mathrm{mistake}\:\mathrm{sir}?? \\ $$
Answered by mind is power last updated on 22/Oct/19
cos(β)=2cos^2 ((β/2))−1=((1−tg^2 ((β/2)))/(1+tg^2 ((β/2)))) assum x≥y x+y#0 β,θ∈[0,π] ((xcos(β)−y)/(x−ycos(β)))=((x(1−tg^2 (β))−y(1+tg^2 ((β/2)))/(x(1+tg^2 (β))−y(1−tg^2 (β))))=(((x−y)−(x+y)tg^2 ((β/2)))/((x−y)+(x+y)tg^2 ((β/2)))) cos(θ)=((1−tg^2 ((θ/2)))/(1+tg^2 ((θ/2))))=(((x−y)−(x+y)tg^2 ((β/2)))/((x−y)+(x+y)tg^2 ((β/2))))=((1−((x+y)/(x−y))tg^2 ((β/2)))/(1+((x+y)/(x−y))tg^2 ((β/2)))) let f(x)=((1−x)/(1+x)) x∈R−{−1}⇒f′(x)=((−2)/((1+x)^2 ))<0 decreasing...I ⇒f(x)=f(y),x=y cos(θ)=((1−tg^2 ((θ/2)))/(1+tg^2 ((θ/2))))=(((x−y)−(x+y)tg^2 ((β/2)))/((x−y)+(x+y)tg^2 ((β/2))))=((1−((x+y)/(x−y))tg^2 ((β/2)))/(1+((x+y)/(x−y))tg^2 ((β/2)))) ⇔f(tg^2 ((θ/2)))=f(((x+y)/(x−y))tg^2 ((β/2)))⇒by I tg^2 ((θ/2))=((x+y)/(x−y))tg^2 ((β/2))⇒tg((θ/2))=(√((x+y)/(x−y)))tg((β/2))
$$\mathrm{cos}\left(\beta\right)=\mathrm{2cos}^{\mathrm{2}} \left(\frac{\beta}{\mathrm{2}}\right)−\mathrm{1}=\frac{\mathrm{1}−\mathrm{tg}^{\mathrm{2}} \left(\frac{\beta}{\mathrm{2}}\right)}{\mathrm{1}+\mathrm{tg}^{\mathrm{2}} \left(\frac{\beta}{\mathrm{2}}\right)} \\ $$$$\mathrm{assum}\:\mathrm{x}\geqslant\mathrm{y}\:\mathrm{x}+\mathrm{y}#\mathrm{0}\:\:\beta,\theta\in\left[\mathrm{0},\pi\right] \\ $$$$\frac{\mathrm{xcos}\left(\beta\right)−\mathrm{y}}{\mathrm{x}−\mathrm{ycos}\left(\beta\right)}=\frac{\mathrm{x}\left(\mathrm{1}−\mathrm{tg}^{\mathrm{2}} \left(\beta\right)\right)−\mathrm{y}\left(\mathrm{1}+\mathrm{tg}^{\mathrm{2}} \left(\frac{\beta}{\mathrm{2}}\right)\right.}{\mathrm{x}\left(\mathrm{1}+\mathrm{tg}^{\mathrm{2}} \left(\beta\right)\right)−\mathrm{y}\left(\mathrm{1}−\mathrm{tg}^{\mathrm{2}} \left(\beta\right)\right)}=\frac{\left(\mathrm{x}−\mathrm{y}\right)−\left(\mathrm{x}+\mathrm{y}\right)\mathrm{tg}^{\mathrm{2}} \left(\frac{\beta}{\mathrm{2}}\right)}{\left(\mathrm{x}−\mathrm{y}\right)+\left(\mathrm{x}+\mathrm{y}\right)\mathrm{tg}^{\mathrm{2}} \left(\frac{\beta}{\mathrm{2}}\right)} \\ $$$$\mathrm{cos}\left(\theta\right)=\frac{\mathrm{1}−\mathrm{tg}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)}{\mathrm{1}+\mathrm{tg}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)}=\frac{\left(\mathrm{x}−\mathrm{y}\right)−\left(\mathrm{x}+\mathrm{y}\right)\mathrm{tg}^{\mathrm{2}} \left(\frac{\beta}{\mathrm{2}}\right)}{\left(\mathrm{x}−\mathrm{y}\right)+\left(\mathrm{x}+\mathrm{y}\right)\mathrm{tg}^{\mathrm{2}} \left(\frac{\beta}{\mathrm{2}}\right)}=\frac{\mathrm{1}−\frac{\mathrm{x}+\mathrm{y}}{\mathrm{x}−\mathrm{y}}\mathrm{tg}^{\mathrm{2}} \left(\frac{\beta}{\mathrm{2}}\right)}{\mathrm{1}+\frac{\mathrm{x}+\mathrm{y}}{\mathrm{x}−\mathrm{y}}\mathrm{tg}^{\mathrm{2}} \left(\frac{\beta}{\mathrm{2}}\right)} \\ $$$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}−\mathrm{x}}{\mathrm{1}+\mathrm{x}}\:\:\:\:\:\mathrm{x}\in\mathbb{R}−\left\{−\mathrm{1}\right\}\Rightarrow\mathrm{f}'\left(\mathrm{x}\right)=\frac{−\mathrm{2}}{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{2}} }<\mathrm{0}\:\mathrm{decreasing}…\mathrm{I} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{y}\right),\mathrm{x}=\mathrm{y} \\ $$$$\mathrm{cos}\left(\theta\right)=\frac{\mathrm{1}−\mathrm{tg}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)}{\mathrm{1}+\mathrm{tg}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)}=\frac{\left(\mathrm{x}−\mathrm{y}\right)−\left(\mathrm{x}+\mathrm{y}\right)\mathrm{tg}^{\mathrm{2}} \left(\frac{\beta}{\mathrm{2}}\right)}{\left(\mathrm{x}−\mathrm{y}\right)+\left(\mathrm{x}+\mathrm{y}\right)\mathrm{tg}^{\mathrm{2}} \left(\frac{\beta}{\mathrm{2}}\right)}=\frac{\mathrm{1}−\frac{\mathrm{x}+\mathrm{y}}{\mathrm{x}−\mathrm{y}}\mathrm{tg}^{\mathrm{2}} \left(\frac{\beta}{\mathrm{2}}\right)}{\mathrm{1}+\frac{\mathrm{x}+\mathrm{y}}{\mathrm{x}−\mathrm{y}}\mathrm{tg}^{\mathrm{2}} \left(\frac{\beta}{\mathrm{2}}\right)} \\ $$$$\Leftrightarrow\mathrm{f}\left(\mathrm{tg}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)\right)=\mathrm{f}\left(\frac{\mathrm{x}+\mathrm{y}}{\mathrm{x}−\mathrm{y}}\mathrm{tg}^{\mathrm{2}} \left(\frac{\beta}{\mathrm{2}}\right)\right)\Rightarrow\mathrm{by}\:\:\mathrm{I} \\ $$$$\mathrm{tg}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)=\frac{\mathrm{x}+\mathrm{y}}{\mathrm{x}−\mathrm{y}}\mathrm{tg}^{\mathrm{2}} \left(\frac{\beta}{\mathrm{2}}\right)\Rightarrow\mathrm{tg}\left(\frac{\theta}{\mathrm{2}}\right)=\sqrt{\frac{\mathrm{x}+\mathrm{y}}{\mathrm{x}−\mathrm{y}}}\mathrm{tg}\left(\frac{\beta}{\mathrm{2}}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by lalitchand last updated on 22/Oct/19
I dont understand sir? if u dont mind tell me easy way
$$\mathrm{I}\:\mathrm{dont}\:\mathrm{understand}\:\mathrm{sir}?\:\mathrm{if}\:\mathrm{u}\:\mathrm{dont}\:\mathrm{mind}\:\mathrm{tell}\:\mathrm{me}\:\mathrm{easy}\:\mathrm{way} \\ $$
Commented by mind is power last updated on 23/Oct/19
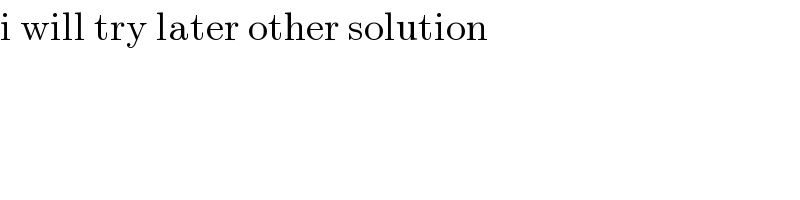
i will try later other solution
$$\mathrm{i}\:\mathrm{will}\:\mathrm{try}\:\mathrm{later}\:\mathrm{other}\:\mathrm{solution}\: \\ $$
Answered by Tanmay chaudhury last updated on 22/Oct/19
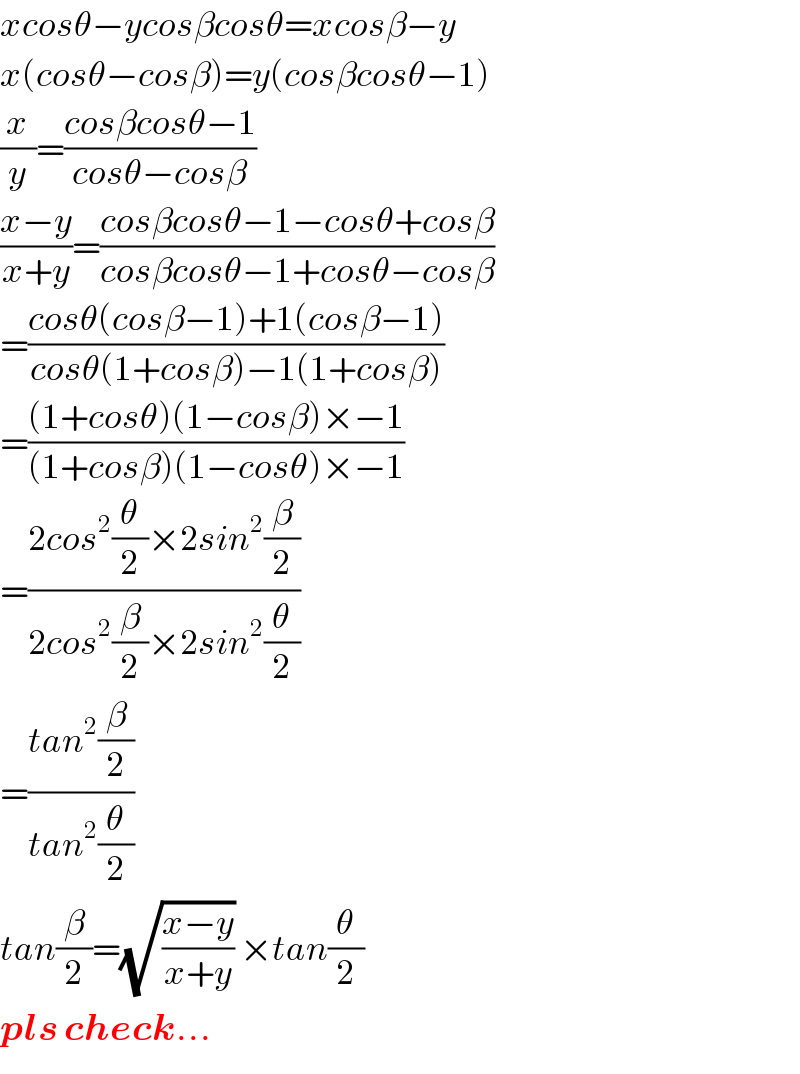
xcosθ−ycosβcosθ=xcosβ−y x(cosθ−cosβ)=y(cosβcosθ−1) (x/y)=((cosβcosθ−1)/(cosθ−cosβ)) ((x−y)/(x+y))=((cosβcosθ−1−cosθ+cosβ)/(cosβcosθ−1+cosθ−cosβ)) =((cosθ(cosβ−1)+1(cosβ−1))/(cosθ(1+cosβ)−1(1+cosβ))) =(((1+cosθ)(1−cosβ)×−1)/((1+cosβ)(1−cosθ)×−1)) =((2cos^2 (θ/2)×2sin^2 (β/2))/(2cos^2 (β/2)×2sin^2 (θ/2))) =((tan^2 (β/2))/(tan^2 (θ/2))) tan(β/2)=(√((x−y)/(x+y))) ×tan(θ/2) pls check...
$${xcos}\theta−{ycos}\beta{cos}\theta={xcos}\beta−{y} \\ $$$${x}\left({cos}\theta−{cos}\beta\right)={y}\left({cos}\beta{cos}\theta−\mathrm{1}\right) \\ $$$$\frac{{x}}{{y}}=\frac{{cos}\beta{cos}\theta−\mathrm{1}}{{cos}\theta−{cos}\beta} \\ $$$$\frac{{x}−{y}}{{x}+{y}}=\frac{{cos}\beta{cos}\theta−\mathrm{1}−{cos}\theta+{cos}\beta}{{cos}\beta{cos}\theta−\mathrm{1}+{cos}\theta−{cos}\beta} \\ $$$$=\frac{{cos}\theta\left({cos}\beta−\mathrm{1}\right)+\mathrm{1}\left({cos}\beta−\mathrm{1}\right)}{{cos}\theta\left(\mathrm{1}+{cos}\beta\right)−\mathrm{1}\left(\mathrm{1}+{cos}\beta\right)} \\ $$$$=\frac{\left(\mathrm{1}+{cos}\theta\right)\left(\mathrm{1}−{cos}\beta\right)×−\mathrm{1}}{\left(\mathrm{1}+{cos}\beta\right)\left(\mathrm{1}−{cos}\theta\right)×−\mathrm{1}} \\ $$$$=\frac{\mathrm{2}{cos}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}×\mathrm{2}{sin}^{\mathrm{2}} \frac{\beta}{\mathrm{2}}}{\mathrm{2}{cos}^{\mathrm{2}} \frac{\beta}{\mathrm{2}}×\mathrm{2}{sin}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}} \\ $$$$=\frac{{tan}^{\mathrm{2}} \frac{\beta}{\mathrm{2}}}{{tan}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}} \\ $$$${tan}\frac{\beta}{\mathrm{2}}=\sqrt{\frac{{x}−{y}}{{x}+{y}}}\:×{tan}\frac{\theta}{\mathrm{2}} \\ $$$$\boldsymbol{{pls}}\:\boldsymbol{{check}}… \\ $$
Commented by mind is power last updated on 23/Oct/19
nice sir creative solution
$$\mathrm{nice}\:\mathrm{sir}\:\:\mathrm{creative}\:\mathrm{solution} \\ $$
Commented by Tanmay chaudhury last updated on 23/Oct/19
thank you sir
$${thank}\:{you}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *