Question Number 140730 by liberty last updated on 12/May/21
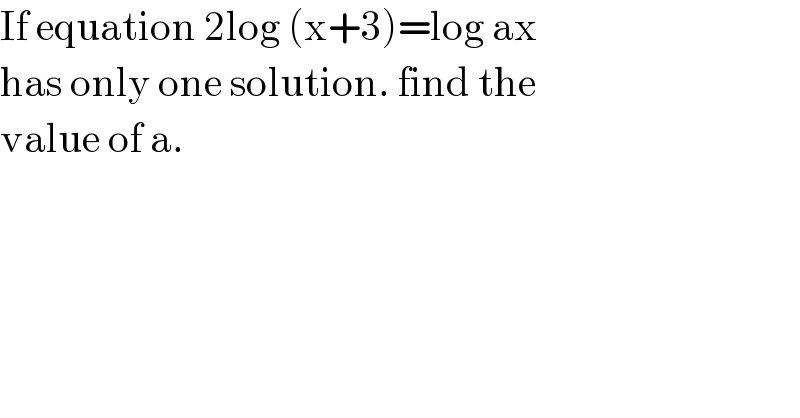
Answered by mr W last updated on 12/May/21
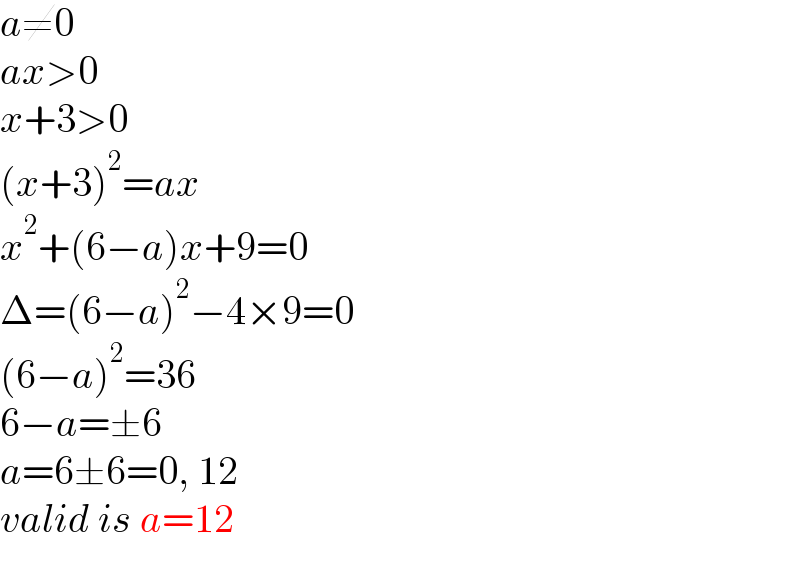
Commented by EDWIN88 last updated on 12/May/21

Commented by EDWIN88 last updated on 12/May/21
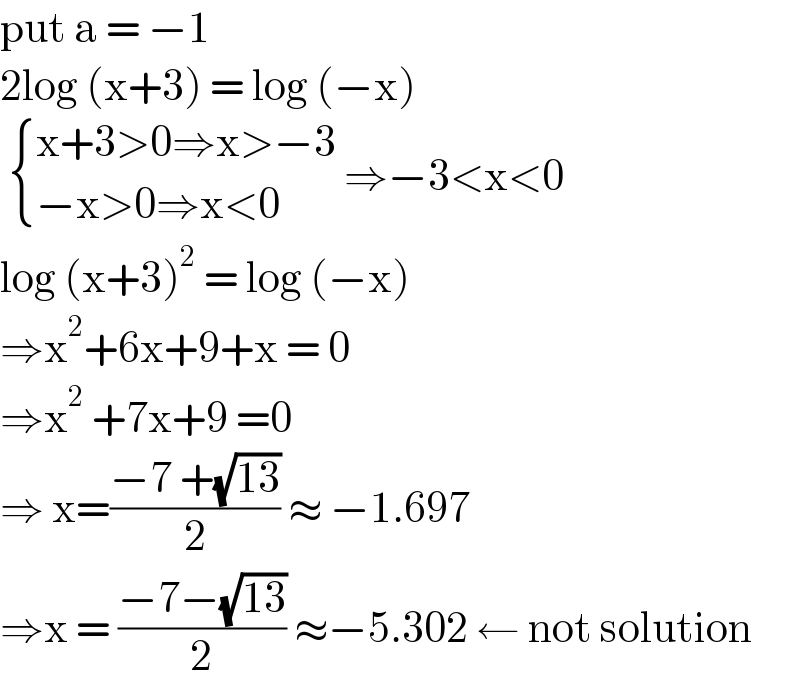
Commented by mr W last updated on 12/May/21