Question Number 652 by 123456 last updated on 19/Feb/15

$${if}\:{f}:\mathbb{R}\rightarrow\mathbb{R}\:{is}\:{continuous}\:{and} \\ $$$${f}\left({x}+{y}\right)={f}\left({x}\right)+{y} \\ $$$$\mathrm{1}.\:{find}\:{f}\left({x}\right) \\ $$$$\mathrm{2}.\:{proof}\:{or}\:{disproof}\:{that}\:{f}'\left({x}\right)=\mathrm{1} \\ $$$$\mathrm{3}.\:{if}\:{f}\left(\mathrm{0}\right)=\mathrm{0}\:{proof}\:{or}\:{disproof}\:{that}\:{f}\left({x}\right)={x} \\ $$
Answered by prakash jain last updated on 19/Feb/15
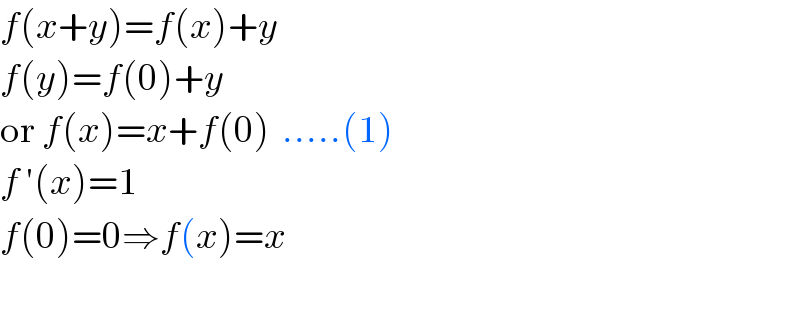
$${f}\left({x}+{y}\right)={f}\left({x}\right)+{y} \\ $$$${f}\left({y}\right)={f}\left(\mathrm{0}\right)+{y} \\ $$$$\mathrm{or}\:{f}\left({x}\right)={x}+{f}\left(\mathrm{0}\right)\:\:…..\left(\mathrm{1}\right) \\ $$$${f}\:'\left({x}\right)=\mathrm{1} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0}\Rightarrow{f}\left({x}\right)={x} \\ $$$$ \\ $$
