Question Number 78468 by Dah Solu Tion last updated on 17/Jan/20
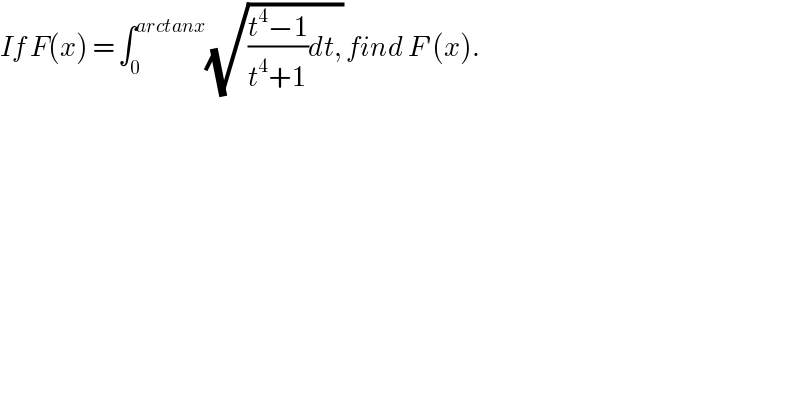
$${If}\:{F}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{{arctanx}} \sqrt{\frac{{t}^{\mathrm{4}} −\mathrm{1}}{{t}^{\mathrm{4}} +\mathrm{1}}{dt},}\:{find}\:{F}'\left({x}\right). \\ $$
Commented by mathmax by abdo last updated on 17/Jan/20
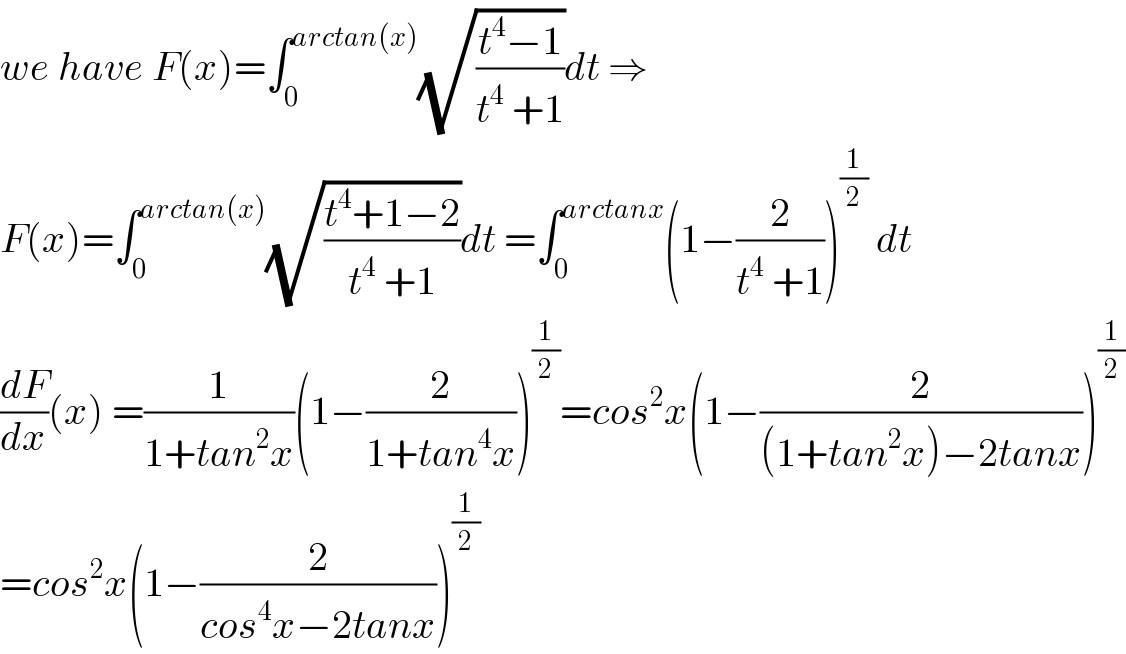
$${we}\:{have}\:{F}\left({x}\right)=\int_{\mathrm{0}} ^{{arctan}\left({x}\right)} \sqrt{\frac{{t}^{\mathrm{4}} −\mathrm{1}}{{t}^{\mathrm{4}} \:+\mathrm{1}}}{dt}\:\Rightarrow \\ $$$${F}\left({x}\right)=\int_{\mathrm{0}} ^{{arctan}\left({x}\right)} \sqrt{\frac{{t}^{\mathrm{4}} +\mathrm{1}−\mathrm{2}}{{t}^{\mathrm{4}} \:+\mathrm{1}}}{dt}\:=\int_{\mathrm{0}} ^{{arctanx}} \left(\mathrm{1}−\frac{\mathrm{2}}{{t}^{\mathrm{4}} \:+\mathrm{1}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:{dt} \\ $$$$\frac{{dF}}{{dx}}\left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+{tan}^{\mathrm{2}} {x}}\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{1}+{tan}^{\mathrm{4}} {x}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} ={cos}^{\mathrm{2}} {x}\left(\mathrm{1}−\frac{\mathrm{2}}{\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)−\mathrm{2}{tanx}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$={cos}^{\mathrm{2}} {x}\left(\mathrm{1}−\frac{\mathrm{2}}{{cos}^{\mathrm{4}} {x}−\mathrm{2}{tanx}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$
