if-f-x-1-x-x-3-1-x-3-then-faind-f-1-x-

Question Number 131573 by mathlove last updated on 06/Feb/21

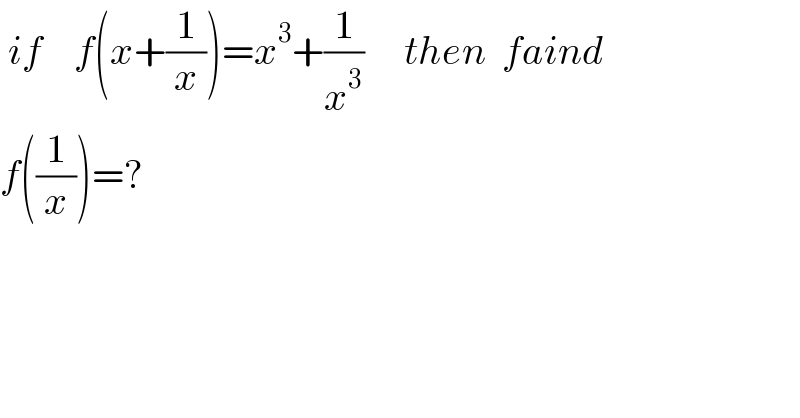
$$\:{if}\:\:\:\:{f}\left({x}+\frac{\mathrm{1}}{{x}}\right)={x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\:\:\:\:\:{then}\:\:{faind}\:\: \\ $$$${f}\left(\frac{\mathrm{1}}{{x}}\right)=? \\ $$

Answered by rs4089 last updated on 06/Feb/21

f(x+(1/x))=x^3 +(1/x^3 ) f(x+(1/x))=(x+(1/x))(x^2 +(1/x^2 )−1) f(x+(1/x))=(x+(1/x)){(x+(1/x))^2 −2−1} f(x+(1/x))=(x+(1/x)){(x+(1/x))^2 −3} now put x+(1/x) = t f(t)=t(t^2 −3) or f(x)=x(x^2 −3) so f((1/x)) =(1/x)((1/x^2 )−3)=((1−3x^2 )/x^3 )

$${f}\left({x}+\frac{\mathrm{1}}{{x}}\right)={x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} } \\ $$$${f}\left({x}+\frac{\mathrm{1}}{{x}}\right)=\left({x}+\frac{\mathrm{1}}{{x}}\right)\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{1}\right) \\ $$$${f}\left({x}+\frac{\mathrm{1}}{{x}}\right)=\left({x}+\frac{\mathrm{1}}{{x}}\right)\left\{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{2}−\mathrm{1}\right\} \\ $$$${f}\left({x}+\frac{\mathrm{1}}{{x}}\right)=\left({x}+\frac{\mathrm{1}}{{x}}\right)\left\{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{3}\right\} \\ $$$${now}\:{put}\:{x}+\frac{\mathrm{1}}{{x}}\:=\:{t}\: \\ $$$${f}\left({t}\right)={t}\left({t}^{\mathrm{2}} −\mathrm{3}\right) \\ $$$${or}\:{f}\left({x}\right)={x}\left({x}^{\mathrm{2}} −\mathrm{3}\right) \\ $$$${so}\:\:{f}\left(\frac{\mathrm{1}}{{x}}\right)\:=\frac{\mathrm{1}}{{x}}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{3}\right)=\frac{\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} }{{x}^{\mathrm{3}} } \\ $$$$ \\ $$

Commented by mathlove last updated on 06/Feb/21

$${tanks} \\ $$

Answered by mathmax by abdo last updated on 06/Feb/21

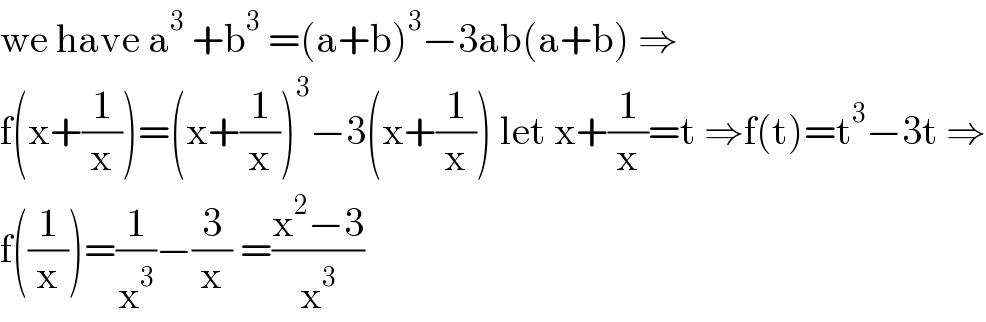
we have a^3 +b^3 =(a+b)^3 −3ab(a+b) ⇒ f(x+(1/x))=(x+(1/x))^3 −3(x+(1/x)) let x+(1/x)=t ⇒f(t)=t^3 −3t ⇒ f((1/x))=(1/x^3 )−(3/x) =((x^2 −3)/x^3 )

$$\mathrm{we}\:\mathrm{have}\:\mathrm{a}^{\mathrm{3}} \:+\mathrm{b}^{\mathrm{3}} \:=\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{3}} −\mathrm{3ab}\left(\mathrm{a}+\mathrm{b}\right)\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)=\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{3}} −\mathrm{3}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)\:\mathrm{let}\:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{t}\:\Rightarrow\mathrm{f}\left(\mathrm{t}\right)=\mathrm{t}^{\mathrm{3}} −\mathrm{3t}\:\Rightarrow \\ $$$$\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }−\frac{\mathrm{3}}{\mathrm{x}}\:=\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{3}}{\mathrm{x}^{\mathrm{3}} } \\ $$

Facebook Tweet Pin

if-f-x-1-x-x-3-1-x-3-then-faind-f-1-x-

Leave a Reply Cancel reply