Question Number 10874 by Saham last updated on 28/Feb/17
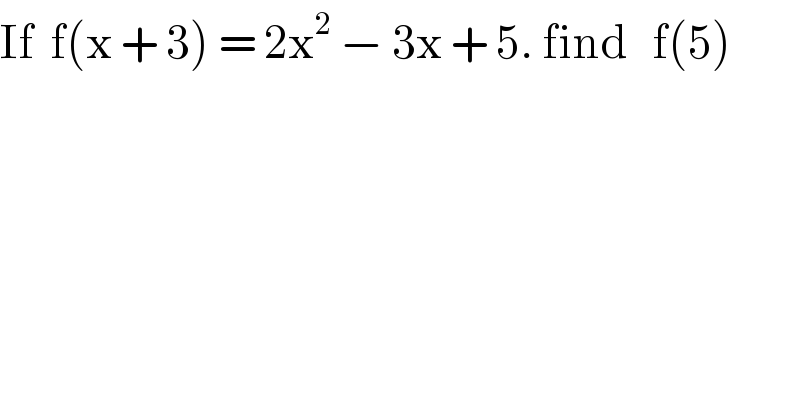
$$\mathrm{If}\:\:\mathrm{f}\left(\mathrm{x}\:+\:\mathrm{3}\right)\:=\:\mathrm{2x}^{\mathrm{2}} \:−\:\mathrm{3x}\:+\:\mathrm{5}.\:\mathrm{find}\:\:\:\mathrm{f}\left(\mathrm{5}\right) \\ $$
Answered by ridwan balatif last updated on 28/Feb/17
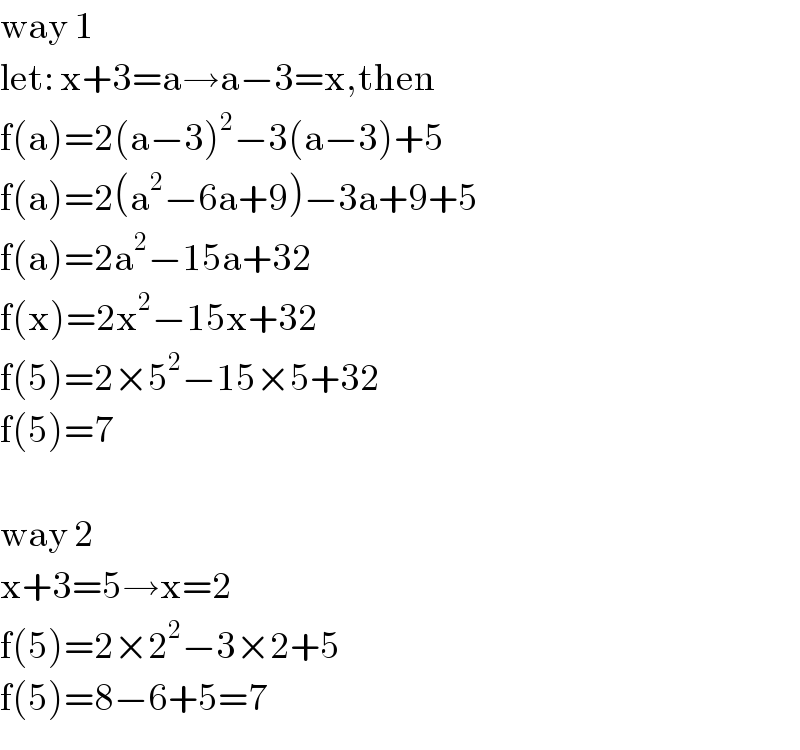
$$\mathrm{way}\:\mathrm{1} \\ $$$$\mathrm{let}:\:\mathrm{x}+\mathrm{3}=\mathrm{a}\rightarrow\mathrm{a}−\mathrm{3}=\mathrm{x},\mathrm{then} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\mathrm{2}\left(\mathrm{a}−\mathrm{3}\right)^{\mathrm{2}} −\mathrm{3}\left(\mathrm{a}−\mathrm{3}\right)+\mathrm{5} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\mathrm{2}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{6a}+\mathrm{9}\right)−\mathrm{3a}+\mathrm{9}+\mathrm{5} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\mathrm{2a}^{\mathrm{2}} −\mathrm{15a}+\mathrm{32} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{2x}^{\mathrm{2}} −\mathrm{15x}+\mathrm{32} \\ $$$$\mathrm{f}\left(\mathrm{5}\right)=\mathrm{2}×\mathrm{5}^{\mathrm{2}} −\mathrm{15}×\mathrm{5}+\mathrm{32} \\ $$$$\mathrm{f}\left(\mathrm{5}\right)=\mathrm{7} \\ $$$$\: \\ $$$$\mathrm{way}\:\mathrm{2} \\ $$$$\mathrm{x}+\mathrm{3}=\mathrm{5}\rightarrow\mathrm{x}=\mathrm{2} \\ $$$$\mathrm{f}\left(\mathrm{5}\right)=\mathrm{2}×\mathrm{2}^{\mathrm{2}} −\mathrm{3}×\mathrm{2}+\mathrm{5} \\ $$$$\mathrm{f}\left(\mathrm{5}\right)=\mathrm{8}−\mathrm{6}+\mathrm{5}=\mathrm{7} \\ $$
Commented by Saham last updated on 28/Feb/17
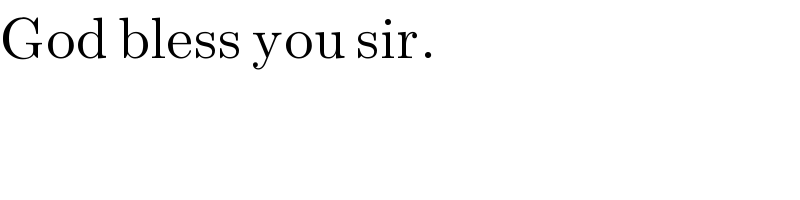
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
