Question Number 143427 by bramlexs22 last updated on 14/Jun/21

$${if}\:{f}\left({x}\right)\:{is}\:{polynomial}\:{satisfying} \\ $$$${f}\left({x}\right){f}\left(\frac{\mathrm{1}}{{x}}\right)−\mathrm{2}{f}\left({x}\right)+\mathrm{2}{f}\left(\frac{\mathrm{1}}{{x}}\right)=\mathrm{5} \\ $$$${and}\:{f}\left(\mathrm{2}\right)=\mathrm{14}\:{then}\:{f}\left(\mathrm{3}\right)=? \\ $$
Answered by qaz last updated on 14/Jun/21
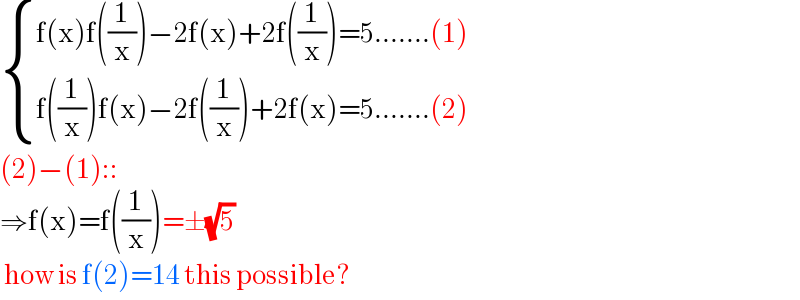
$$\begin{cases}{\mathrm{f}\left(\mathrm{x}\right)\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)−\mathrm{2f}\left(\mathrm{x}\right)+\mathrm{2f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\mathrm{5}…….\left(\mathrm{1}\right)}\\{\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\mathrm{f}\left(\mathrm{x}\right)−\mathrm{2f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)+\mathrm{2f}\left(\mathrm{x}\right)=\mathrm{5}…….\left(\mathrm{2}\right)}\end{cases} \\ $$$$\left(\mathrm{2}\right)−\left(\mathrm{1}\right):: \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\pm\sqrt{\mathrm{5}} \\ $$$$\:\mathrm{how}\:\mathrm{is}\:\mathrm{f}\left(\mathrm{2}\right)=\mathrm{14}\:\mathrm{this}\:\mathrm{possible}? \\ $$
