Question Number 143959 by bobhans last updated on 20/Jun/21
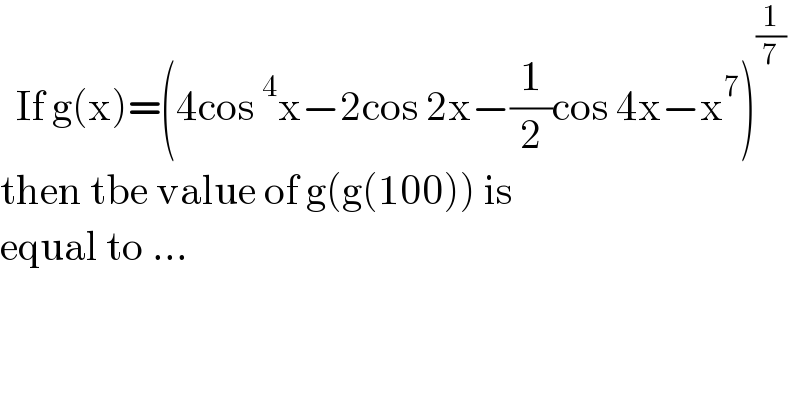
$$\:\:\mathrm{If}\:\mathrm{g}\left(\mathrm{x}\right)=\left(\mathrm{4cos}\:^{\mathrm{4}} \mathrm{x}−\mathrm{2cos}\:\mathrm{2x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{4x}−\mathrm{x}^{\mathrm{7}} \right)^{\frac{\mathrm{1}}{\mathrm{7}}} \\ $$$$\mathrm{then}\:\mathrm{tbe}\:\mathrm{value}\:\mathrm{of}\:\mathrm{g}\left(\mathrm{g}\left(\mathrm{100}\right)\right)\:\mathrm{is} \\ $$$$\mathrm{equal}\:\mathrm{to}\:… \\ $$
Answered by Olaf_Thorendsen last updated on 20/Jun/21
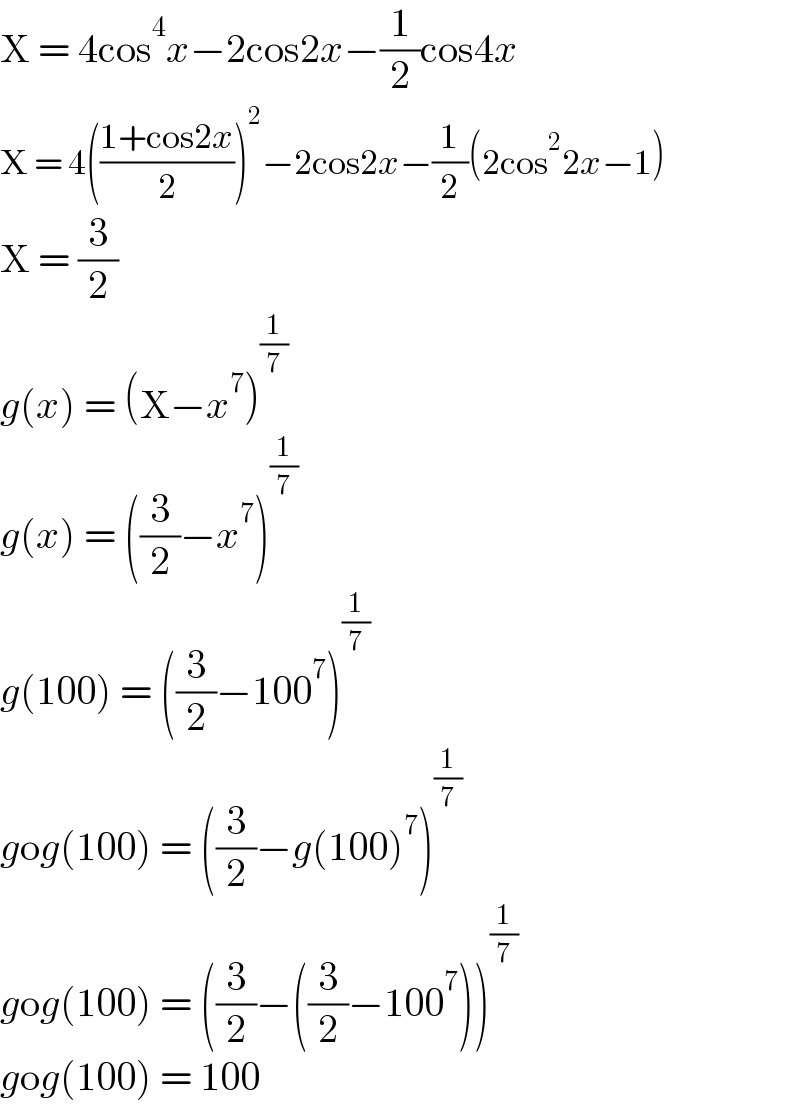
$$\mathrm{X}\:=\:\mathrm{4cos}^{\mathrm{4}} {x}−\mathrm{2cos2}{x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos4}{x} \\ $$$$\mathrm{X}\:=\:\mathrm{4}\left(\frac{\mathrm{1}+\mathrm{cos2}{x}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{2cos2}{x}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2cos}^{\mathrm{2}} \mathrm{2}{x}−\mathrm{1}\right) \\ $$$$\mathrm{X}\:=\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${g}\left({x}\right)\:=\:\left(\mathrm{X}−{x}^{\mathrm{7}} \right)^{\frac{\mathrm{1}}{\mathrm{7}}} \\ $$$${g}\left({x}\right)\:=\:\left(\frac{\mathrm{3}}{\mathrm{2}}−{x}^{\mathrm{7}} \right)^{\frac{\mathrm{1}}{\mathrm{7}}} \\ $$$${g}\left(\mathrm{100}\right)\:=\:\left(\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{100}^{\mathrm{7}} \right)^{\frac{\mathrm{1}}{\mathrm{7}}} \\ $$$${g}\mathrm{o}{g}\left(\mathrm{100}\right)\:=\:\left(\frac{\mathrm{3}}{\mathrm{2}}−{g}\left(\mathrm{100}\right)^{\mathrm{7}} \right)^{\frac{\mathrm{1}}{\mathrm{7}}} \\ $$$${g}\mathrm{o}{g}\left(\mathrm{100}\right)\:=\:\left(\frac{\mathrm{3}}{\mathrm{2}}−\left(\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{100}^{\mathrm{7}} \right)\right)^{\frac{\mathrm{1}}{\mathrm{7}}} \\ $$$${g}\mathrm{o}{g}\left(\mathrm{100}\right)\:=\:\mathrm{100} \\ $$
