Question Number 78458 by kaivan.ahmadi last updated on 17/Jan/20
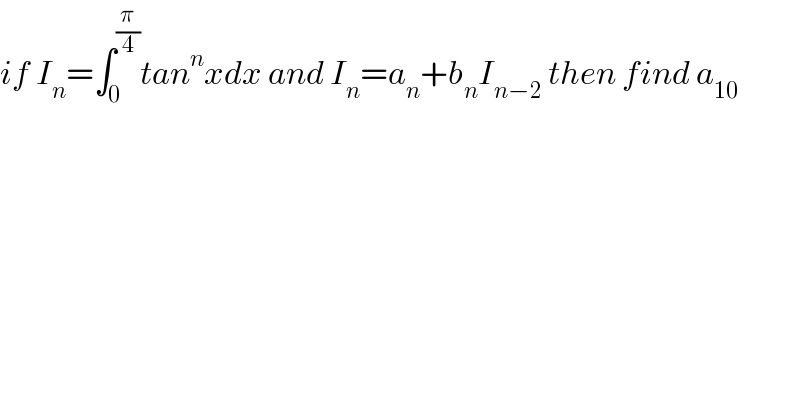
$${if}\:{I}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {tan}^{{n}} {xdx}\:{and}\:{I}_{{n}} ={a}_{{n}} +{b}_{{n}} {I}_{{n}−\mathrm{2}} \:{then}\:{find}\:{a}_{\mathrm{10}} \\ $$
Commented by kaivan.ahmadi last updated on 17/Jan/20
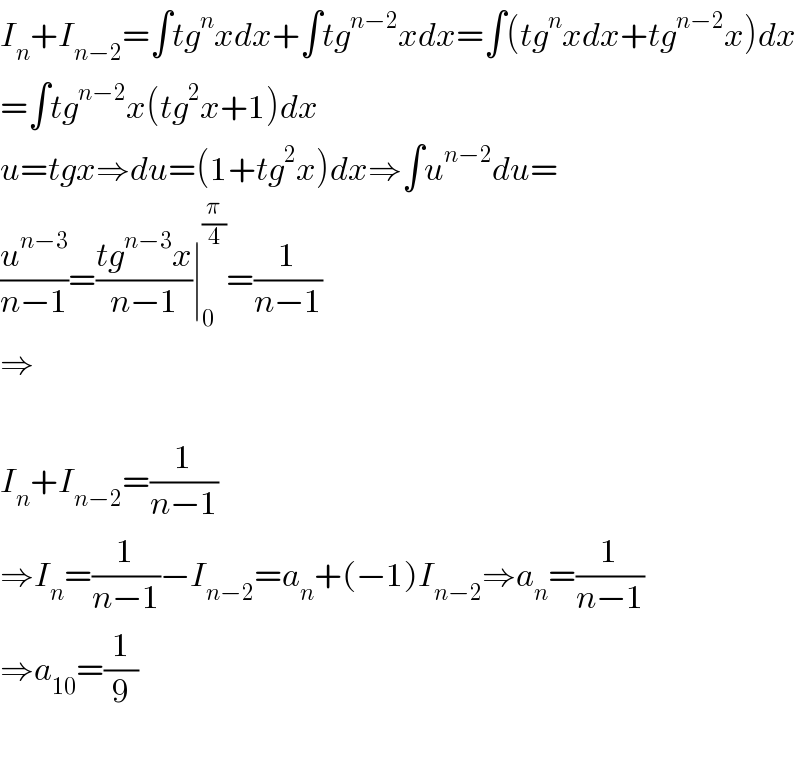
$${I}_{{n}} +{I}_{{n}−\mathrm{2}} =\int{tg}^{{n}} {xdx}+\int{tg}^{{n}−\mathrm{2}} {xdx}=\int\left({tg}^{{n}} {xdx}+{tg}^{{n}−\mathrm{2}} {x}\right){dx} \\ $$$$=\int{tg}^{{n}−\mathrm{2}} {x}\left({tg}^{\mathrm{2}} {x}+\mathrm{1}\right){dx} \\ $$$${u}={tgx}\Rightarrow{du}=\left(\mathrm{1}+{tg}^{\mathrm{2}} {x}\right){dx}\Rightarrow\int{u}^{{n}−\mathrm{2}} {du}= \\ $$$$\frac{{u}^{{n}−\mathrm{3}} }{{n}−\mathrm{1}}=\frac{{tg}^{{n}−\mathrm{3}} {x}}{{n}−\mathrm{1}}\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} =\frac{\mathrm{1}}{{n}−\mathrm{1}} \\ $$$$\Rightarrow \\ $$$$ \\ $$$${I}_{{n}} +{I}_{{n}−\mathrm{2}} =\frac{\mathrm{1}}{{n}−\mathrm{1}} \\ $$$$\Rightarrow{I}_{{n}} =\frac{\mathrm{1}}{{n}−\mathrm{1}}−{I}_{{n}−\mathrm{2}} ={a}_{{n}} +\left(−\mathrm{1}\right){I}_{{n}−\mathrm{2}} \Rightarrow{a}_{{n}} =\frac{\mathrm{1}}{{n}−\mathrm{1}} \\ $$$$\Rightarrow{a}_{\mathrm{10}} =\frac{\mathrm{1}}{\mathrm{9}} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 17/Jan/20
![I_n =∫_0 ^(π/4) tan^n x dx ⇒ I_n =∫_0 ^(π/4) tan^(n−2) x (1+tan^2 x−1)dx =∫_0 ^(π/4) (1+tan^2 x)tan^(n−2) x dx−∫_0 ^(π/4) tan^(n−2) x dx =[(1/(n−1))tan^(n−1) x]_0 ^(π/4) −I_(n−2) =(1/(n−1)) −I_(n−2) if n≥2 ⇒a_n =(1/(n−1)) and b_n =−1 ⇒a_(10) =(1/9) let calculate I_n interms of n we have I_n +I_(n−2) =(1/(n−1)) ⇒I_(2n) +I_(2n−2) =(1/(2n−1)) let I_(2n) =u_n ⇒ u_n +u_(n−1) =(1/(2n−1)) ⇒Σ_(k=1) ^n (−1)^k (u_k +u_(k−1) ) =Σ_(k=1) ^n (((−1)^k )/(2k−1)) ⇒ −(u_1 +u_0 )+u_2 +u_1 +....(−1)^n (u_n +u_(n−1) )=Σ_(k=1) ^n (((−1)^k )/(2k−1)) (−1)^n u_n −u_0 =Σ_(k=1) ^n (((−1)^k )/(2k−1)) ⇒(−1)^n u_n =u_0 +Σ_(k=1) ^n (((−1)^k )/(2k−1)) ⇒ u_n =(−1)^n u_0 +(−1)^n Σ_(k=1) ^n (((−1)^k )/(2k−1)) =(π/4)(−1)^n +(−1)^n Σ_(k=1) ^n (((−1)^k )/(2k−1)) ⇒I_(2n) =(π/4)(−1)^n +(−1)^n Σ_(k=1) ^n (((−1)^k )/(2k−1)) let detemine I_(2n+1) ? we have I_(2n+1) +I_(2n−1) =(1/(2n)) ⇒Σ_(k=1) ^n (−1)^k (v_k +v_(k−1) )=Σ_(k=1) ^n (((−1)^k )/(2k)) (v_n =I_(2n+1) ) ⇒(−1)^n v_n −v_0 =Σ_(k=1) ^n (((−1)^k )/(2k)) ⇒ (−1)^n v_n =v_0 +Σ_(k=1) ^n (((−1)^k )/(2k)) ⇒ v_n =(−1)^n v_0 +(−1)^n Σ_(k=1) ^n (((−1)^k )/(2k)) v_0 =I_1 =∫_0 ^(π/4) tanx dx =−∫_0 ^(π/4) ((−sinx)/(cosx))dx =−ln∣cosx∣]_0 ^(π/4) =−ln((1/( (√2)))) =(1/2)ln(2) ⇒I_(2n+1) =(−1)^n ((ln(2))/2) +(−1)^n Σ_(k=1) ^n (((−1)^k )/(2k))](https://www.tinkutara.com/question/Q78470.png)
$${I}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{tan}^{{n}} {x}\:{dx}\:\Rightarrow\:{I}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {tan}^{{n}−\mathrm{2}} {x}\:\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}−\mathrm{1}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right){tan}^{{n}−\mathrm{2}} {x}\:{dx}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{tan}^{{n}−\mathrm{2}} {x}\:{dx} \\ $$$$=\left[\frac{\mathrm{1}}{{n}−\mathrm{1}}{tan}^{{n}−\mathrm{1}} {x}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} −{I}_{{n}−\mathrm{2}} =\frac{\mathrm{1}}{{n}−\mathrm{1}}\:−{I}_{{n}−\mathrm{2}} \:\:\:{if}\:{n}\geqslant\mathrm{2}\:\Rightarrow{a}_{{n}} =\frac{\mathrm{1}}{{n}−\mathrm{1}} \\ $$$${and}\:{b}_{{n}} =−\mathrm{1}\:\Rightarrow{a}_{\mathrm{10}} =\frac{\mathrm{1}}{\mathrm{9}} \\ $$$${let}\:{calculate}\:{I}_{{n}} \:{interms}\:{of}\:{n}\:{we}\:{have} \\ $$$${I}_{{n}} +{I}_{{n}−\mathrm{2}} =\frac{\mathrm{1}}{{n}−\mathrm{1}}\:\Rightarrow{I}_{\mathrm{2}{n}} \:+{I}_{\mathrm{2}{n}−\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}\:{let}\:{I}_{\mathrm{2}{n}} ={u}_{{n}} \:\Rightarrow \\ $$$${u}_{{n}} +{u}_{{n}−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}\:\Rightarrow\sum_{{k}=\mathrm{1}} ^{{n}} \left(−\mathrm{1}\right)^{{k}} \left({u}_{{k}} +{u}_{{k}−\mathrm{1}} \right)\:=\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{k}−\mathrm{1}}\:\Rightarrow \\ $$$$−\left({u}_{\mathrm{1}} +{u}_{\mathrm{0}} \right)+{u}_{\mathrm{2}} +{u}_{\mathrm{1}} \:+….\left(−\mathrm{1}\right)^{{n}} \left({u}_{{n}} \:+{u}_{{n}−\mathrm{1}} \right)=\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{k}−\mathrm{1}} \\ $$$$\left(−\mathrm{1}\right)^{{n}} {u}_{{n}} −{u}_{\mathrm{0}} =\sum_{{k}=\mathrm{1}} ^{{n}} \frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{k}−\mathrm{1}}\:\Rightarrow\left(−\mathrm{1}\right)^{{n}} {u}_{{n}} ={u}_{\mathrm{0}} \:+\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{k}−\mathrm{1}}\:\Rightarrow \\ $$$${u}_{{n}} =\left(−\mathrm{1}\right)^{{n}} {u}_{\mathrm{0}} \:+\left(−\mathrm{1}\right)^{{n}} \sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{k}−\mathrm{1}}\:=\frac{\pi}{\mathrm{4}}\left(−\mathrm{1}\right)^{{n}} \:+\left(−\mathrm{1}\right)^{{n}} \sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{k}−\mathrm{1}} \\ $$$$\Rightarrow{I}_{\mathrm{2}{n}} =\frac{\pi}{\mathrm{4}}\left(−\mathrm{1}\right)^{{n}} \:+\left(−\mathrm{1}\right)^{{n}} \:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{k}−\mathrm{1}}\:\:\:\:{let}\:{detemine}\:{I}_{\mathrm{2}{n}+\mathrm{1}} ? \\ $$$${we}\:{have}\:{I}_{\mathrm{2}{n}+\mathrm{1}} +{I}_{\mathrm{2}{n}−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}{n}}\:\Rightarrow\sum_{{k}=\mathrm{1}} ^{{n}} \left(−\mathrm{1}\right)^{{k}} \left({v}_{{k}} \:+{v}_{{k}−\mathrm{1}} \right)=\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{k}} \\ $$$$\left({v}_{{n}} ={I}_{\mathrm{2}{n}+\mathrm{1}} \right)\:\Rightarrow\left(−\mathrm{1}\right)^{{n}} {v}_{{n}} −{v}_{\mathrm{0}} \:=\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{k}}\:\Rightarrow \\ $$$$\left(−\mathrm{1}\right)^{{n}} \:{v}_{{n}} ={v}_{\mathrm{0}} \:+\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{k}}\:\Rightarrow \\ $$$${v}_{{n}} =\left(−\mathrm{1}\right)^{{n}} {v}_{\mathrm{0}} \:+\left(−\mathrm{1}\right)^{{n}} \:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{k}} \\ $$$$\left.{v}_{\mathrm{0}} ={I}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{tanx}\:{dx}\:=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{−{sinx}}{{cosx}}{dx}\:=−{ln}\mid{cosx}\mid\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=−{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:\Rightarrow{I}_{\mathrm{2}{n}+\mathrm{1}} =\left(−\mathrm{1}\right)^{{n}} \frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\:+\left(−\mathrm{1}\right)^{{n}} \sum_{{k}=\mathrm{1}} ^{{n}} \frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{k}} \\ $$
