Question Number 75484 by vishalbhardwaj last updated on 11/Dec/19
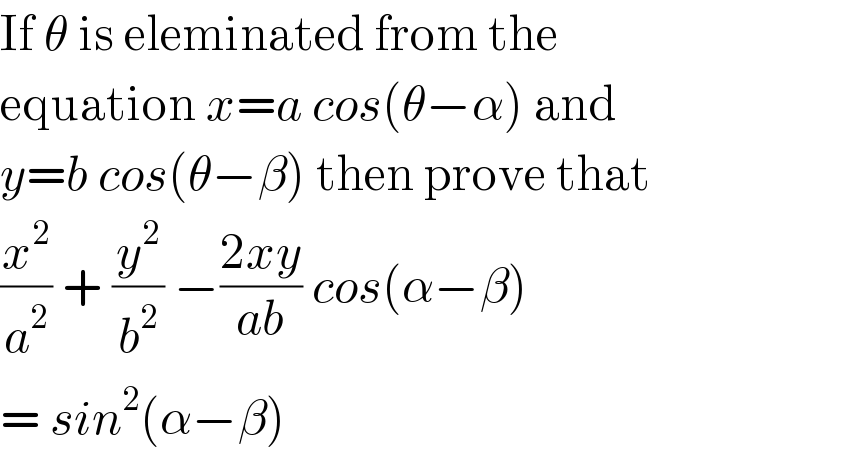
$$\mathrm{If}\:\theta\:\mathrm{is}\:\mathrm{eleminated}\:\mathrm{from}\:\mathrm{the} \\ $$$$\mathrm{equation}\:{x}={a}\:{cos}\left(\theta−\alpha\right)\:\mathrm{and} \\ $$$${y}={b}\:{cos}\left(\theta−\beta\right)\:\mathrm{then}\:\mathrm{prove}\:\mathrm{that} \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\:+\:\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:−\frac{\mathrm{2}{xy}}{{ab}}\:{cos}\left(\alpha−\beta\right)\: \\ $$$$=\:{sin}^{\mathrm{2}} \left(\alpha−\beta\right) \\ $$
Answered by MJS last updated on 12/Dec/19
![x=acos (θ−α) ⇒ θ=α−arccos (x/a) y=bcos (α−β−arccos (x/a)) [cos (u+v) =cos u cos v −sin u sin v] [sin (u+v) =cos u sin v −sin u cos v] y=(b/a)xcos (α−β)±(b/a)(√(a^2 −x^2 ))sin (α−β) (x^2 /a^2 )+(y^2 /b^2 )−((2xy)/(ab))cos (α−β) =sin^2 (α−β) ⇒ y=(b/a)xcos (α−β)±(b/a)(√(a^2 −x^2 ))sin (α−β) same as above ⇒ proved](https://www.tinkutara.com/question/Q75491.png)
$${x}={a}\mathrm{cos}\:\left(\theta−\alpha\right)\:\Rightarrow\:\theta=\alpha−\mathrm{arccos}\:\frac{{x}}{{a}} \\ $$$${y}={b}\mathrm{cos}\:\left(\alpha−\beta−\mathrm{arccos}\:\frac{{x}}{{a}}\right) \\ $$$$\:\:\:\:\:\left[\mathrm{cos}\:\left({u}+{v}\right)\:=\mathrm{cos}\:{u}\:\mathrm{cos}\:{v}\:−\mathrm{sin}\:{u}\:\mathrm{sin}\:{v}\right] \\ $$$$\:\:\:\:\:\left[\mathrm{sin}\:\left({u}+{v}\right)\:=\mathrm{cos}\:{u}\:\mathrm{sin}\:{v}\:\:−\mathrm{sin}\:{u}\:\mathrm{cos}\:{v}\right] \\ $$$${y}=\frac{{b}}{{a}}{x}\mathrm{cos}\:\left(\alpha−\beta\right)\pm\frac{{b}}{{a}}\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\mathrm{sin}\:\left(\alpha−\beta\right) \\ $$$$ \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\frac{\mathrm{2}{xy}}{{ab}}\mathrm{cos}\:\left(\alpha−\beta\right)\:=\mathrm{sin}^{\mathrm{2}} \:\left(\alpha−\beta\right) \\ $$$$\Rightarrow\:{y}=\frac{{b}}{{a}}{x}\mathrm{cos}\:\left(\alpha−\beta\right)\pm\frac{{b}}{{a}}\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\mathrm{sin}\:\left(\alpha−\beta\right) \\ $$$$\mathrm{same}\:\mathrm{as}\:\mathrm{above}\:\Rightarrow\:\mathrm{proved} \\ $$
