Question Number 12328 by Mr Chheang Chantria last updated on 19/Apr/17
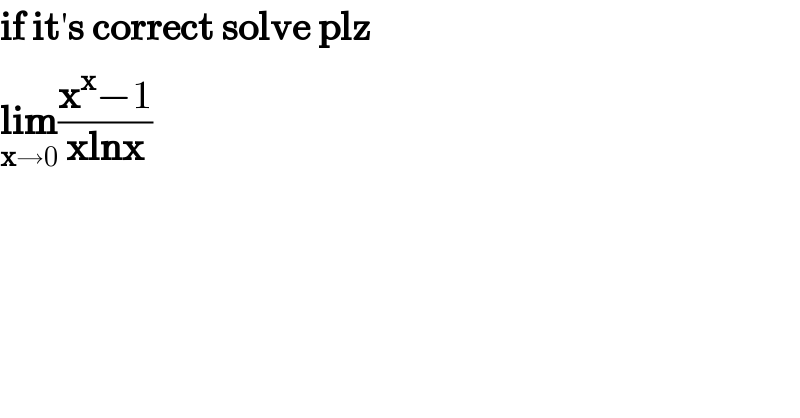
$$\boldsymbol{\mathrm{if}}\:\boldsymbol{\mathrm{it}}'\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{correct}}\:\boldsymbol{\mathrm{solve}}\:\boldsymbol{\mathrm{plz}} \\ $$$$\underset{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{0}} {\boldsymbol{\mathrm{lim}}}\frac{\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}} −\mathrm{1}}{\boldsymbol{\mathrm{xlnx}}} \\ $$
Answered by mrW1 last updated on 19/Apr/17
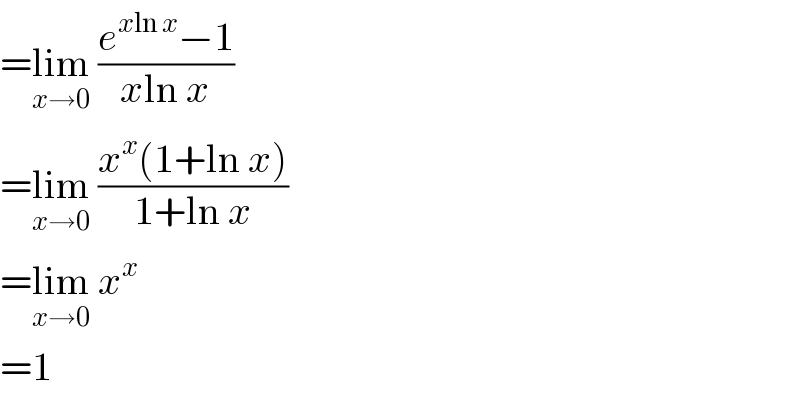
$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{e}^{{x}\mathrm{ln}\:{x}} −\mathrm{1}}{{x}\mathrm{ln}\:{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{{x}} \left(\mathrm{1}+\mathrm{ln}\:{x}\right)}{\mathrm{1}+\mathrm{ln}\:{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{x}^{{x}} \\ $$$$=\mathrm{1} \\ $$
