Question Number 73200 by aliesam last updated on 07/Nov/19
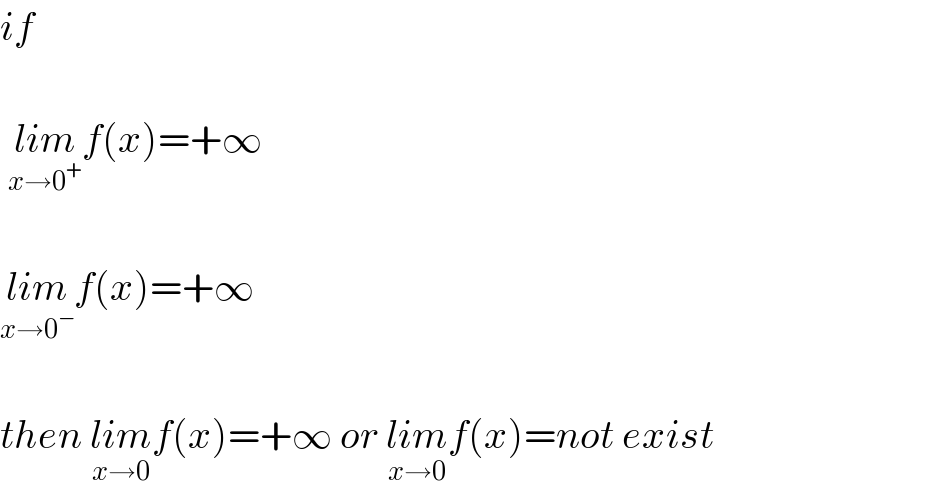
$${if}\:\: \\ $$$$ \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}^{+} } {{lim}f}\left({x}\right)=+\infty \\ $$$$ \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{−} } {{lim}f}\left({x}\right)=+\infty \\ $$$$ \\ $$$${then}\:\underset{{x}\rightarrow\mathrm{0}} {{lim}f}\left({x}\right)=+\infty\:{or}\:\underset{{x}\rightarrow\mathrm{0}} {{lim}f}\left({x}\right)={not}\:{exist} \\ $$
Commented by kaivan.ahmadi last updated on 08/Nov/19

$${lim}_{{x}\rightarrow\mathrm{0}} {f}\left({x}\right)=+\infty \\ $$
Commented by aliesam last updated on 08/Nov/19
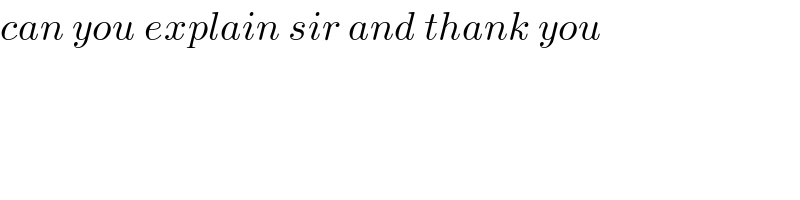
$${can}\:{you}\:{explain}\:{sir}\:{and}\:{thank}\:{you} \\ $$
Commented by kaivan.ahmadi last updated on 08/Nov/19

$${this}\:{is}\:{definition}\:{of}\:{infinite}\:{limits}. \\ $$$${infinite}\:{limits}\:{are}\:{those}\:{that}\:{have}\:{a}\:{value} \\ $$$${of}\:\pm\infty,{where}\:{the}\:{function}\:{grows}\:{without} \\ $$$${bound}\:{as}\:{it}\:{approaches}\:{some}\:{value}\:{a}.{for}\:{f}\left({x}\right) \\ $$$${as},\:{x}\:{approaches}\:{a},{the}\:{infinite}\:{limit}\:{is}\:{shown} \\ $$$${as}\:{lim}_{{x}\rightarrow{a}} {f}\left({x}\right)=\infty. \\ $$
Commented by aliesam last updated on 08/Nov/19
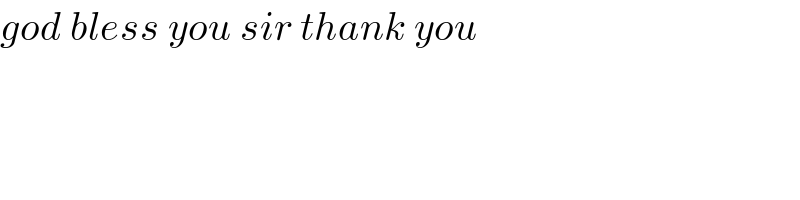
$${god}\:{bless}\:{you}\:{sir}\:{thank}\:{you} \\ $$
