Question Number 65972 by gunawan last updated on 07/Aug/19
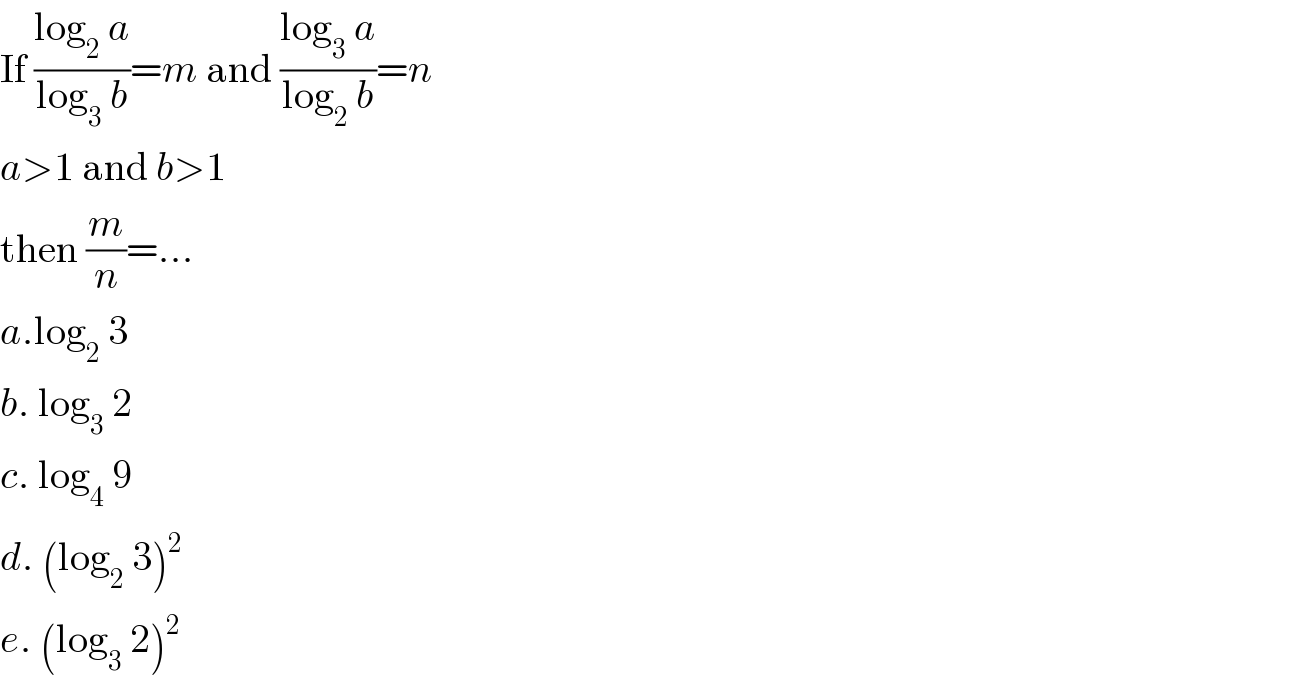
$$\mathrm{If}\:\frac{\mathrm{log}_{\mathrm{2}} \:{a}}{\mathrm{log}_{\mathrm{3}} \:{b}}={m}\:\mathrm{and}\:\frac{\mathrm{log}_{\mathrm{3}} \:{a}}{\mathrm{log}_{\mathrm{2}} \:{b}}={n} \\ $$$${a}>\mathrm{1}\:\mathrm{and}\:{b}>\mathrm{1} \\ $$$$\mathrm{then}\:\frac{{m}}{{n}}=… \\ $$$${a}.\mathrm{log}_{\mathrm{2}} \:\mathrm{3} \\ $$$${b}.\:\mathrm{log}_{\mathrm{3}} \:\mathrm{2} \\ $$$${c}.\:\mathrm{log}_{\mathrm{4}} \:\mathrm{9} \\ $$$${d}.\:\left(\mathrm{log}_{\mathrm{2}} \:\mathrm{3}\right)^{\mathrm{2}} \\ $$$${e}.\:\left(\mathrm{log}_{\mathrm{3}} \:\mathrm{2}\right)^{\mathrm{2}} \\ $$
Answered by MJS last updated on 07/Aug/19
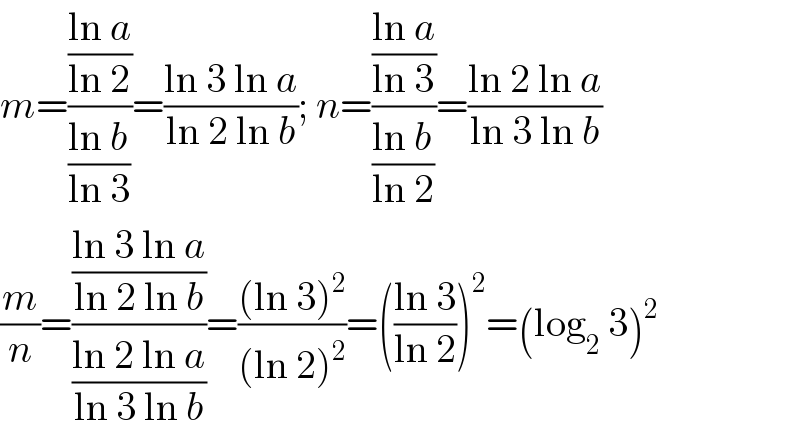
$${m}=\frac{\frac{\mathrm{ln}\:{a}}{\mathrm{ln}\:\mathrm{2}}}{\frac{\mathrm{ln}\:{b}}{\mathrm{ln}\:\mathrm{3}}}=\frac{\mathrm{ln}\:\mathrm{3}\:\mathrm{ln}\:{a}}{\mathrm{ln}\:\mathrm{2}\:\mathrm{ln}\:{b}};\:{n}=\frac{\frac{\mathrm{ln}\:{a}}{\mathrm{ln}\:\mathrm{3}}}{\frac{\mathrm{ln}\:{b}}{\mathrm{ln}\:\mathrm{2}}}=\frac{\mathrm{ln}\:\mathrm{2}\:\mathrm{ln}\:{a}}{\mathrm{ln}\:\mathrm{3}\:\mathrm{ln}\:{b}} \\ $$$$\frac{{m}}{{n}}=\frac{\frac{\mathrm{ln}\:\mathrm{3}\:\mathrm{ln}\:{a}}{\mathrm{ln}\:\mathrm{2}\:\mathrm{ln}\:{b}}}{\frac{\mathrm{ln}\:\mathrm{2}\:\mathrm{ln}\:{a}}{\mathrm{ln}\:\mathrm{3}\:\mathrm{ln}\:{b}}}=\frac{\left(\mathrm{ln}\:\mathrm{3}\right)^{\mathrm{2}} }{\left(\mathrm{ln}\:\mathrm{2}\right)^{\mathrm{2}} }=\left(\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{2}}\right)^{\mathrm{2}} =\left(\mathrm{log}_{\mathrm{2}} \:\mathrm{3}\right)^{\mathrm{2}} \\ $$
