Question Number 8164 by 666225 last updated on 02/Oct/16

$${if}\:\boldsymbol{{p}}\:{is}\:{prima}\:{show}\:{that}\:\sqrt{\boldsymbol{{p}}}\:{irasional} \\ $$
Commented by 123456 last updated on 02/Oct/16

$$\mathrm{1}\mid{p},{p}\mid{p},{p}>\mathrm{1} \\ $$$${p}\mid{a}^{\mathrm{2}} \Leftrightarrow{p}\mid{a} \\ $$
Commented by 123456 last updated on 02/Oct/16
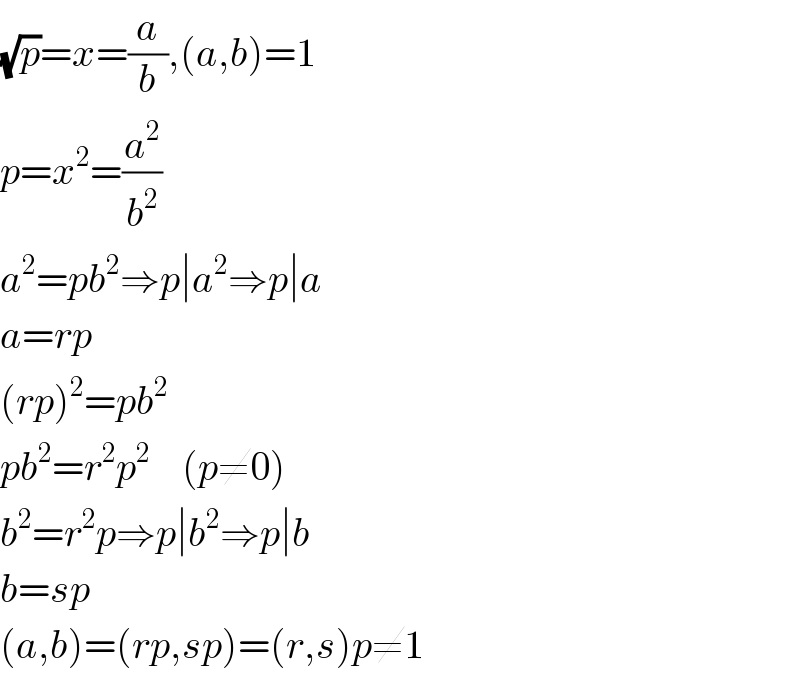
$$\sqrt{{p}}={x}=\frac{{a}}{{b}},\left({a},{b}\right)=\mathrm{1} \\ $$$${p}={x}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$${a}^{\mathrm{2}} ={pb}^{\mathrm{2}} \Rightarrow{p}\mid{a}^{\mathrm{2}} \Rightarrow{p}\mid{a} \\ $$$${a}={rp} \\ $$$$\left({rp}\right)^{\mathrm{2}} ={pb}^{\mathrm{2}} \\ $$$${pb}^{\mathrm{2}} ={r}^{\mathrm{2}} {p}^{\mathrm{2}} \:\:\:\:\left({p}\neq\mathrm{0}\right) \\ $$$${b}^{\mathrm{2}} ={r}^{\mathrm{2}} {p}\Rightarrow{p}\mid{b}^{\mathrm{2}} \Rightarrow{p}\mid{b} \\ $$$${b}={sp} \\ $$$$\left({a},{b}\right)=\left({rp},{sp}\right)=\left({r},{s}\right){p}\neq\mathrm{1} \\ $$
Answered by prakash jain last updated on 02/Oct/16
$$\mathrm{answer}\:\mathrm{in}\:\mathrm{comments}. \\ $$
