if-p-x-is-a-polynomial-and-p-x-p-1-x-p-x-p-1-x-p-3-28-then-p-x-p-4-

Question Number 806 by 123456 last updated on 16/Mar/15

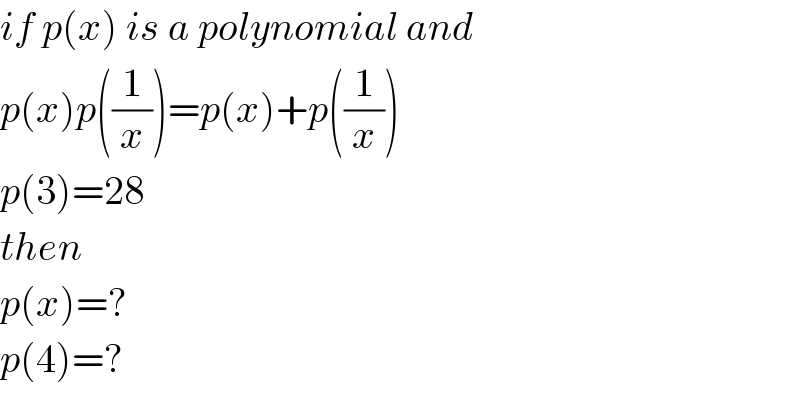
$${if}\:{p}\left({x}\right)\:{is}\:{a}\:{polynomial}\:{and} \\ $$$${p}\left({x}\right){p}\left(\frac{\mathrm{1}}{{x}}\right)={p}\left({x}\right)+{p}\left(\frac{\mathrm{1}}{{x}}\right) \\ $$$${p}\left(\mathrm{3}\right)=\mathrm{28} \\ $$$${then} \\ $$$${p}\left({x}\right)=? \\ $$$${p}\left(\mathrm{4}\right)=? \\ $$

Commented by 123456 last updated on 16/Mar/15

x=±1⇒(1/x)=±1 p(±1)p(±1)=p(±1)+p(±1) [p(±1)]^2 −2p(±1)=0 p(±1)[p(±1)−2]=0 p(±1)=0∨p(±1)=2

$${x}=\pm\mathrm{1}\Rightarrow\frac{\mathrm{1}}{{x}}=\pm\mathrm{1} \\ $$$${p}\left(\pm\mathrm{1}\right){p}\left(\pm\mathrm{1}\right)={p}\left(\pm\mathrm{1}\right)+{p}\left(\pm\mathrm{1}\right) \\ $$$$\left[{p}\left(\pm\mathrm{1}\right)\right]^{\mathrm{2}} −\mathrm{2}{p}\left(\pm\mathrm{1}\right)=\mathrm{0} \\ $$$${p}\left(\pm\mathrm{1}\right)\left[{p}\left(\pm\mathrm{1}\right)−\mathrm{2}\right]=\mathrm{0} \\ $$$${p}\left(\pm\mathrm{1}\right)=\mathrm{0}\vee{p}\left(\pm\mathrm{1}\right)=\mathrm{2} \\ $$

Commented by prakash jain last updated on 16/Mar/15

p(x)=Σ_(i=0) ^n a_i x^i p(x)p((1/x))=p(x)+p((1/x)) Equating coefficients for x^(−n) a_0 a_n =a_n ⇒a_0 =1 Equating coefficients for x^0 a_0 ^2 +a_1 ^2 +...+a_n ^2 =2a_0 a_1 ^2 +...+a_n ^2 =1 ....(i) Equating coefficients for x^1 a_0 a_1 +a_1 a_2 +..+a_(n−1) a_n =a_1 a_1 a_2 +a_2 a_3 +..+a_(n−1) a_n =0 Equating coefficients for x^2 a_1 a_3 +a_2 a_4 +..+a_(n−2) a_n =0 Equating coefficent for x^(n−1) a_0 a_(n−1) +a_1 a_n =a_(n−1) a_0 =1 hence a_1 a_n =0 a_n ≠0 (poynomial of degree n) hence a_1 =0 So all coefficient (a_1 ...a_(n−1) )= 0. From (i) a_n =1 p(x)=1+x^n p(x)p((1/x))=(1+x^n )(1+(1/x^n ))=1+x^n +(1/x^n )+1 =p(x)+p((1/x)) p(3)=28=1+3^n ⇒n=3 p(4)=1+4^3 =65

$${p}\left({x}\right)=\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{i}} {x}^{{i}} \\ $$$${p}\left({x}\right){p}\left(\frac{\mathrm{1}}{{x}}\right)={p}\left({x}\right)+{p}\left(\frac{\mathrm{1}}{{x}}\right) \\ $$$$\mathrm{Equating}\:\mathrm{coefficients}\:\mathrm{for}\:{x}^{−{n}} \\ $$$${a}_{\mathrm{0}} {a}_{{n}} ={a}_{{n}} \Rightarrow{a}_{\mathrm{0}} =\mathrm{1} \\ $$$$\mathrm{Equating}\:\mathrm{coefficients}\:\mathrm{for}\:{x}^{\mathrm{0}} \\ $$$${a}_{\mathrm{0}} ^{\mathrm{2}} +{a}_{\mathrm{1}} ^{\mathrm{2}} +…+{a}_{{n}} ^{\mathrm{2}} =\mathrm{2}{a}_{\mathrm{0}} \\ $$$${a}_{\mathrm{1}} ^{\mathrm{2}} +…+{a}_{{n}} ^{\mathrm{2}} =\mathrm{1}\:\:\:\:\:\:\:\:\:….\left(\mathrm{i}\right) \\ $$$$\mathrm{Equating}\:\mathrm{coefficients}\:\mathrm{for}\:{x}^{\mathrm{1}} \\ $$$${a}_{\mathrm{0}} {a}_{\mathrm{1}} +{a}_{\mathrm{1}} {a}_{\mathrm{2}} +..+{a}_{{n}−\mathrm{1}} {a}_{{n}} ={a}_{\mathrm{1}} \\ $$$${a}_{\mathrm{1}} {a}_{\mathrm{2}} +{a}_{\mathrm{2}} {a}_{\mathrm{3}} +..+{a}_{{n}−\mathrm{1}} {a}_{{n}} =\mathrm{0} \\ $$$$\mathrm{Equating}\:\mathrm{coefficients}\:\mathrm{for}\:{x}^{\mathrm{2}} \\ $$$${a}_{\mathrm{1}} {a}_{\mathrm{3}} +{a}_{\mathrm{2}} {a}_{\mathrm{4}} +..+{a}_{{n}−\mathrm{2}} {a}_{{n}} =\mathrm{0} \\ $$$$\mathrm{Equating}\:\mathrm{coefficent}\:\mathrm{for}\:{x}^{{n}−\mathrm{1}} \\ $$$${a}_{\mathrm{0}} {a}_{{n}−\mathrm{1}} +{a}_{\mathrm{1}} {a}_{{n}} ={a}_{{n}−\mathrm{1}} \\ $$$${a}_{\mathrm{0}} =\mathrm{1}\:\mathrm{hence}\:{a}_{\mathrm{1}} {a}_{{n}} =\mathrm{0} \\ $$$${a}_{{n}} \neq\mathrm{0}\:\left(\mathrm{poynomial}\:\mathrm{of}\:\mathrm{degree}\:{n}\right)\:\mathrm{hence}\:{a}_{\mathrm{1}} =\mathrm{0} \\ $$$$\mathrm{So}\:\mathrm{all}\:\mathrm{coefficient}\:\left({a}_{\mathrm{1}} …{a}_{{n}−\mathrm{1}} \right)=\:\mathrm{0}.\: \\ $$$$\mathrm{From}\:\left(\mathrm{i}\right)\:{a}_{{n}} \:=\mathrm{1} \\ $$$${p}\left({x}\right)=\mathrm{1}+{x}^{{n}} \\ $$$${p}\left({x}\right){p}\left(\frac{\mathrm{1}}{{x}}\right)=\left(\mathrm{1}+{x}^{{n}} \right)\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{{n}} }\right)=\mathrm{1}+{x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:={p}\left({x}\right)+{p}\left(\frac{\mathrm{1}}{{x}}\right) \\ $$$${p}\left(\mathrm{3}\right)=\mathrm{28}=\mathrm{1}+\mathrm{3}^{{n}} \Rightarrow{n}=\mathrm{3} \\ $$$${p}\left(\mathrm{4}\right)=\mathrm{1}+\mathrm{4}^{\mathrm{3}} =\mathrm{65} \\ $$

Answered by prakash jain last updated on 16/Mar/15

See comments p(x)=1+x^3 p(1)=2 p(−1)=0 p(4)=65

$$\mathrm{See}\:\mathrm{comments} \\ $$$${p}\left({x}\right)=\mathrm{1}+{x}^{\mathrm{3}} \\ $$$${p}\left(\mathrm{1}\right)=\mathrm{2} \\ $$$${p}\left(−\mathrm{1}\right)=\mathrm{0} \\ $$$${p}\left(\mathrm{4}\right)=\mathrm{65} \\ $$

Facebook Tweet Pin

if-p-x-is-a-polynomial-and-p-x-p-1-x-p-x-p-1-x-p-3-28-then-p-x-p-4-

Leave a Reply Cancel reply