Question Number 6558 by Tawakalitu. last updated on 02/Jul/16
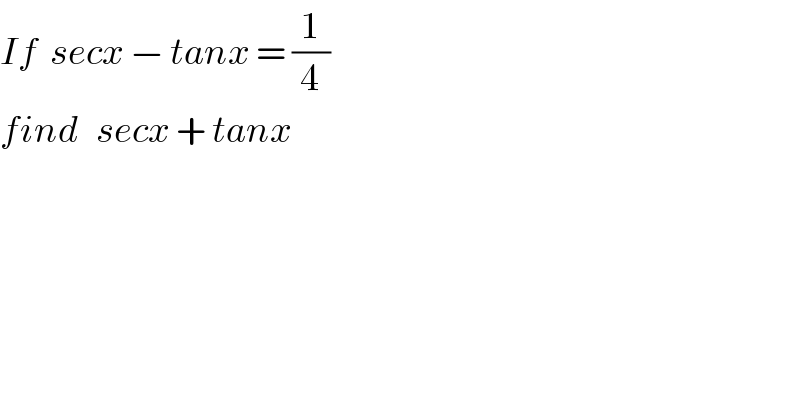
$${If}\:\:{secx}\:−\:{tanx}\:=\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${find}\:\:\:{secx}\:+\:{tanx} \\ $$
Commented by Tawakalitu. last updated on 02/Jul/16

$$ \\ $$$$ \\ $$
Answered by Yozzii last updated on 02/Jul/16
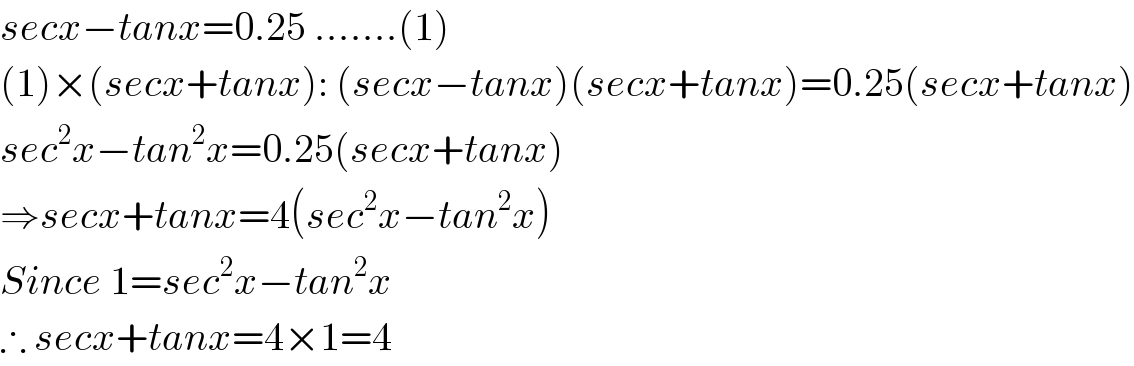
$${secx}−{tanx}=\mathrm{0}.\mathrm{25}\:…….\left(\mathrm{1}\right) \\ $$$$\left(\mathrm{1}\right)×\left({secx}+{tanx}\right):\:\left({secx}−{tanx}\right)\left({secx}+{tanx}\right)=\mathrm{0}.\mathrm{25}\left({secx}+{tanx}\right) \\ $$$${sec}^{\mathrm{2}} {x}−{tan}^{\mathrm{2}} {x}=\mathrm{0}.\mathrm{25}\left({secx}+{tanx}\right) \\ $$$$\Rightarrow{secx}+{tanx}=\mathrm{4}\left({sec}^{\mathrm{2}} {x}−{tan}^{\mathrm{2}} {x}\right) \\ $$$${Since}\:\mathrm{1}={sec}^{\mathrm{2}} {x}−{tan}^{\mathrm{2}} {x} \\ $$$$\therefore\:{secx}+{tanx}=\mathrm{4}×\mathrm{1}=\mathrm{4} \\ $$
Commented by Yozzii last updated on 02/Jul/16
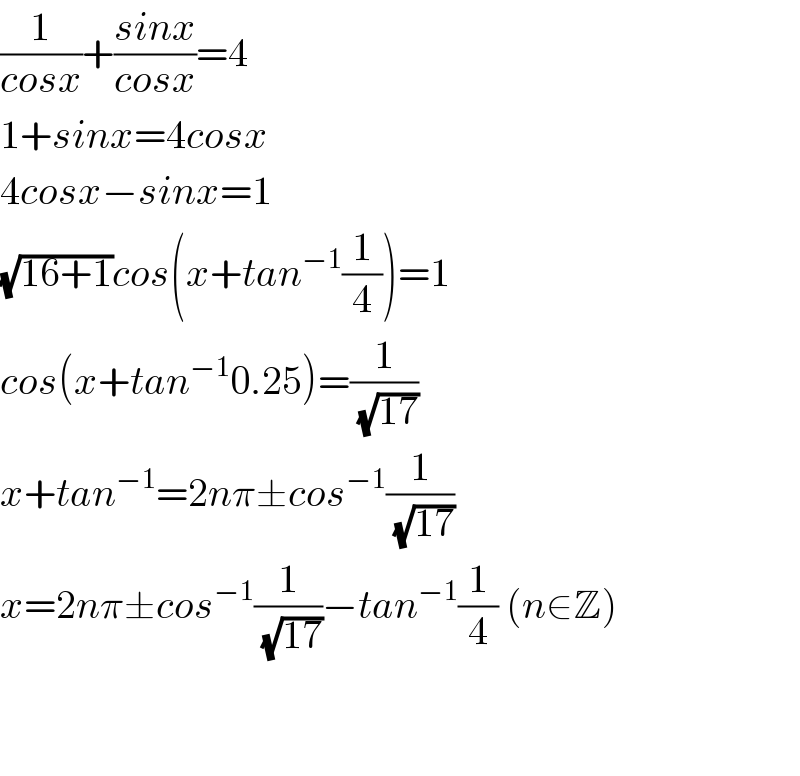
$$\frac{\mathrm{1}}{{cosx}}+\frac{{sinx}}{{cosx}}=\mathrm{4} \\ $$$$\mathrm{1}+{sinx}=\mathrm{4}{cosx} \\ $$$$\mathrm{4}{cosx}−{sinx}=\mathrm{1} \\ $$$$\sqrt{\mathrm{16}+\mathrm{1}}{cos}\left({x}+{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{4}}\right)=\mathrm{1} \\ $$$${cos}\left({x}+{tan}^{−\mathrm{1}} \mathrm{0}.\mathrm{25}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{17}}} \\ $$$${x}+{tan}^{−\mathrm{1}} =\mathrm{2}{n}\pi\pm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{17}}} \\ $$$${x}=\mathrm{2}{n}\pi\pm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{17}}}−{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{4}}\:\left({n}\in\mathbb{Z}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by Tawakalitu. last updated on 03/Jul/16

$${Thanks} \\ $$
