Menu Close

If-sin-1-sin-sin-sin-1-sin-sin-pi-2-find-the-value-of-sin-2-sin-2-1-2-

Tinku Tara 0 Comments
Pin




Question Number 137530 by ZiYangLee last updated on 03/Apr/21
If sin^(−1) (sin α+sin β)+sin^(−1) (sin α−sin β)=(π/2) find the value of sin^2 α+sin^2 β. [(1/2)]
$$\mathrm{If}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{sin}\:\alpha+\mathrm{sin}\:\beta\right)+\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{sin}\:\alpha−\mathrm{sin}\:\beta\right)=\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{sin}^{\mathrm{2}} \alpha+\mathrm{sin}^{\mathrm{2}} \beta.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\frac{\mathrm{1}}{\mathrm{2}}\right] \\ $$
Answered by mr W last updated on 04/Apr/21
sin α+sin β=u sin α−sin β=v sin^2 α+sin^2 β=((u^2 +v^2 )/2) sin^(−1) u+sin^(−1) v=(π/2) sin^(−1) u=(π/2)−sin^(−1) v u=sin ((π/2)−sin^(−1) v)=cos (sin^(−1) v) =(√(1−sin^2 (sin^(−1) v)))=(√(1−v^2 )) ⇒u^2 =1−v^2 ⇒u^2 +v^2 =1 ⇒sin^2 α+sin^2 β=((u^2 +v^2 )/2)=(1/2)
$$\mathrm{sin}\:\alpha+\mathrm{sin}\:\beta={u} \\ $$$$\mathrm{sin}\:\alpha−\mathrm{sin}\:\beta={v} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:\alpha+\mathrm{sin}^{\mathrm{2}} \:\beta=\frac{{u}^{\mathrm{2}} +{v}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{sin}^{−\mathrm{1}} {u}+\mathrm{sin}^{−\mathrm{1}} {v}=\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{sin}^{−\mathrm{1}} {u}=\frac{\pi}{\mathrm{2}}−\mathrm{sin}^{−\mathrm{1}} {v} \\ $$$${u}=\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\mathrm{sin}^{−\mathrm{1}} {v}\right)=\mathrm{cos}\:\left(\mathrm{sin}^{−\mathrm{1}} {v}\right) \\ $$$$\:\:\:=\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\left(\mathrm{sin}^{−\mathrm{1}} {v}\right)}=\sqrt{\mathrm{1}−{v}^{\mathrm{2}} } \\ $$$$\Rightarrow{u}^{\mathrm{2}} =\mathrm{1}−{v}^{\mathrm{2}} \\ $$$$\Rightarrow{u}^{\mathrm{2}} +{v}^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow\mathrm{sin}^{\mathrm{2}} \:\alpha+\mathrm{sin}^{\mathrm{2}} \:\beta=\frac{{u}^{\mathrm{2}} +{v}^{\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by otchereabdullai@gmail.com last updated on 04/Apr/21
prof i want to learn something from you can you please prove the sin^2 A+sin^2 B=1 for me? i only know of sin^2 A+cos^2 A=1 sorry for worrying you
$$\mathrm{prof}\:\mathrm{i}\:\mathrm{want}\:\mathrm{to}\:\mathrm{learn}\:\mathrm{something}\:\mathrm{from}\: \\ $$$$\mathrm{you}\:\mathrm{can}\:\mathrm{you}\:\mathrm{please}\:\mathrm{prove}\:\mathrm{the}\: \\ $$$$\mathrm{sin}^{\mathrm{2}} \mathrm{A}+\mathrm{sin}^{\mathrm{2}} \mathrm{B}=\mathrm{1}\:\mathrm{for}\:\mathrm{me}? \\ $$$$\mathrm{i}\:\mathrm{only}\:\mathrm{know}\:\mathrm{of}\:\mathrm{sin}^{\mathrm{2}} \mathrm{A}+\mathrm{cos}^{\mathrm{2}} \mathrm{A}=\mathrm{1} \\ $$$$\mathrm{sorry}\:\mathrm{for}\:\mathrm{worrying}\:\mathrm{you} \\ $$$$ \\ $$
Commented by otchereabdullai@gmail.com last updated on 04/Apr/21
wow!
$$\mathrm{wow}! \\ $$
Commented by otchereabdullai@gmail.com last updated on 04/Apr/21
very nice solution but am finding it difficult to understand where the cos and the square root is introduce please help me
$$\mathrm{very}\:\mathrm{nice}\:\mathrm{solution}\:\mathrm{but}\:\mathrm{am}\:\mathrm{finding}\:\mathrm{it}\: \\ $$$$\mathrm{difficult}\:\mathrm{to}\:\mathrm{understand}\:\mathrm{where}\:\mathrm{the}\:\mathrm{cos} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{square}\:\mathrm{root}\:\mathrm{is}\:\mathrm{introduce}\: \\ $$$$\mathrm{please}\:\mathrm{help}\:\mathrm{me} \\ $$
Commented by mr W last updated on 04/Apr/21
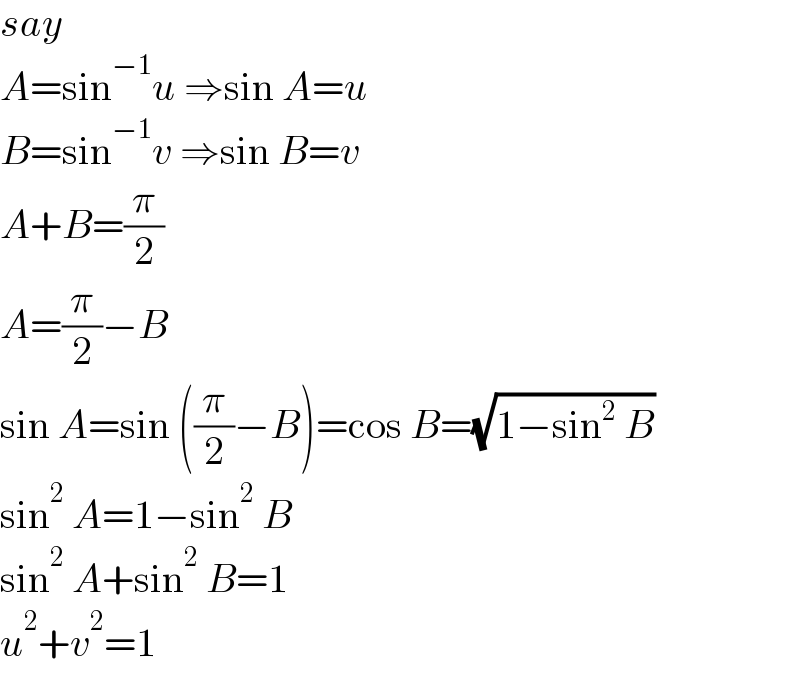
say A=sin^(−1) u ⇒sin A=u B=sin^(−1) v ⇒sin B=v A+B=(π/2) A=(π/2)−B sin A=sin ((π/2)−B)=cos B=(√(1−sin^2 B)) sin^2 A=1−sin^2 B sin^2 A+sin^2 B=1 u^2 +v^2 =1
$${say} \\ $$$${A}=\mathrm{sin}^{−\mathrm{1}} {u}\:\Rightarrow\mathrm{sin}\:{A}={u} \\ $$$${B}=\mathrm{sin}^{−\mathrm{1}} {v}\:\Rightarrow\mathrm{sin}\:{B}={v} \\ $$$${A}+{B}=\frac{\pi}{\mathrm{2}} \\ $$$${A}=\frac{\pi}{\mathrm{2}}−{B} \\ $$$$\mathrm{sin}\:{A}=\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−{B}\right)=\mathrm{cos}\:{B}=\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{B}} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:{A}=\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{B} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:{A}+\mathrm{sin}^{\mathrm{2}} \:{B}=\mathrm{1} \\ $$$${u}^{\mathrm{2}} +{v}^{\mathrm{2}} =\mathrm{1} \\ $$
Commented by otchereabdullai@gmail.com last updated on 04/Apr/21
now is very clear God bless you alot for the kindness profW
$$\mathrm{now}\:\mathrm{is}\:\mathrm{very}\:\mathrm{clear}\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{alot}\: \\ $$$$\mathrm{for}\:\mathrm{the}\:\mathrm{kindness}\:\mathrm{profW} \\ $$
Commented by mr W last updated on 04/Apr/21
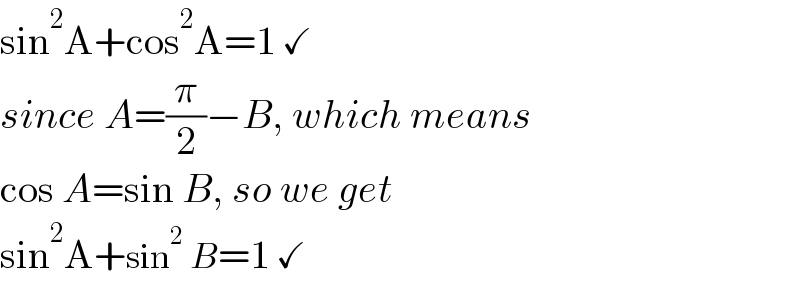
sin^2 A+cos^2 A=1 ✓ since A=(π/2)−B, which means cos A=sin B, so we get sin^2 A+sin^2 B=1 ✓
$$\mathrm{sin}^{\mathrm{2}} \mathrm{A}+\mathrm{cos}^{\mathrm{2}} \mathrm{A}=\mathrm{1}\:\checkmark \\ $$$${since}\:{A}=\frac{\pi}{\mathrm{2}}−{B},\:{which}\:{means}\: \\ $$$$\mathrm{cos}\:{A}=\mathrm{sin}\:{B},\:{so}\:{we}\:{get} \\ $$$$\mathrm{sin}^{\mathrm{2}} \mathrm{A}+\mathrm{sin}^{\mathrm{2}} \:{B}=\mathrm{1}\:\checkmark \\ $$
Commented by otchereabdullai@gmail.com last updated on 04/Apr/21
God bless u profW
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{u}\:\mathrm{profW} \\ $$
Commented by ZiYangLee last updated on 10/Apr/21
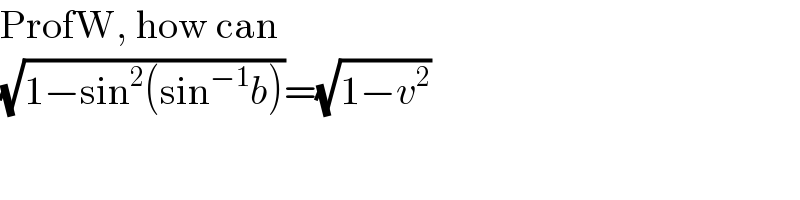
ProfW, how can (√(1−sin^2 (sin^(−1) b)))=(√(1−v^2 ))
$$\mathrm{ProfW},\:\mathrm{how}\:\mathrm{can}\: \\ $$$$\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \left(\mathrm{sin}^{−\mathrm{1}} {b}\right)}=\sqrt{\mathrm{1}−{v}^{\mathrm{2}} } \\ $$
Commented by mr W last updated on 16/Apr/21
you mean (√(1−sin^2 (sin^(−1) v)))=(√(1−v^2 )) ? say sin^(−1) v=V, that means sin V=v i.e. sin (sin^(−1) v)=v so sin^2 (sin^(−1) v)=v^2 (√(1−sin^2 (sin^(−1) v)))=(√(1−v^2 ))
$${you}\:{mean} \\ $$$$\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \left(\mathrm{sin}^{−\mathrm{1}} {v}\right)}=\sqrt{\mathrm{1}−{v}^{\mathrm{2}} }\:? \\ $$$${say}\:\mathrm{sin}^{−\mathrm{1}} {v}={V},\:{that}\:{means} \\ $$$$\mathrm{sin}\:{V}={v} \\ $$$${i}.{e}.\:\mathrm{sin}\:\left(\mathrm{sin}^{−\mathrm{1}} {v}\right)={v} \\ $$$${so}\:\mathrm{sin}^{\mathrm{2}} \:\left(\mathrm{sin}^{−\mathrm{1}} {v}\right)={v}^{\mathrm{2}} \\ $$$$\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \left(\mathrm{sin}^{−\mathrm{1}} {v}\right)}=\sqrt{\mathrm{1}−{v}^{\mathrm{2}} } \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *