Menu Close

If-sin-23pi-24-2-p-q-1-4-r-then-the-value-of-p-2-q-2-r-2-is-equal-to-

Tinku Tara 0 Comments
Pin




Question Number 133142 by bemath last updated on 19/Feb/21
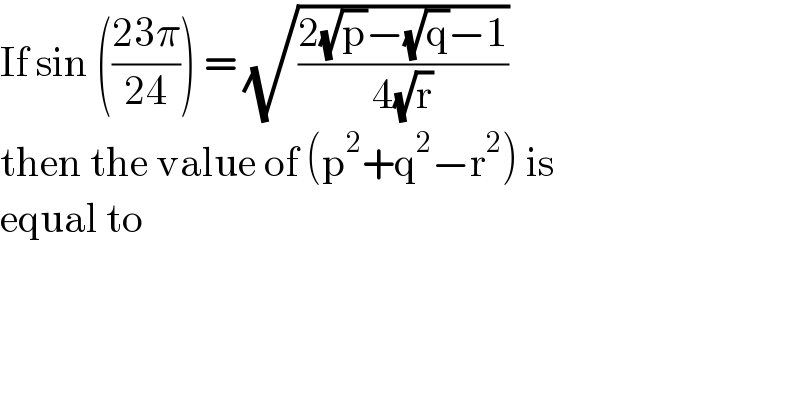
If sin (((23π)/(24))) = (√((2(√p)−(√q)−1)/(4(√r)))) then the value of (p^2 +q^2 −r^2 ) is equal to
$$\mathrm{If}\:\mathrm{sin}\:\left(\frac{\mathrm{23}\pi}{\mathrm{24}}\right)\:=\:\sqrt{\frac{\mathrm{2}\sqrt{\mathrm{p}}−\sqrt{\mathrm{q}}−\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{r}}}} \\ $$$$\mathrm{then}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\left(\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} −\mathrm{r}^{\mathrm{2}} \right)\:\mathrm{is} \\ $$$$\mathrm{equal}\:\mathrm{to}\: \\ $$
Answered by Ñï= last updated on 19/Feb/21
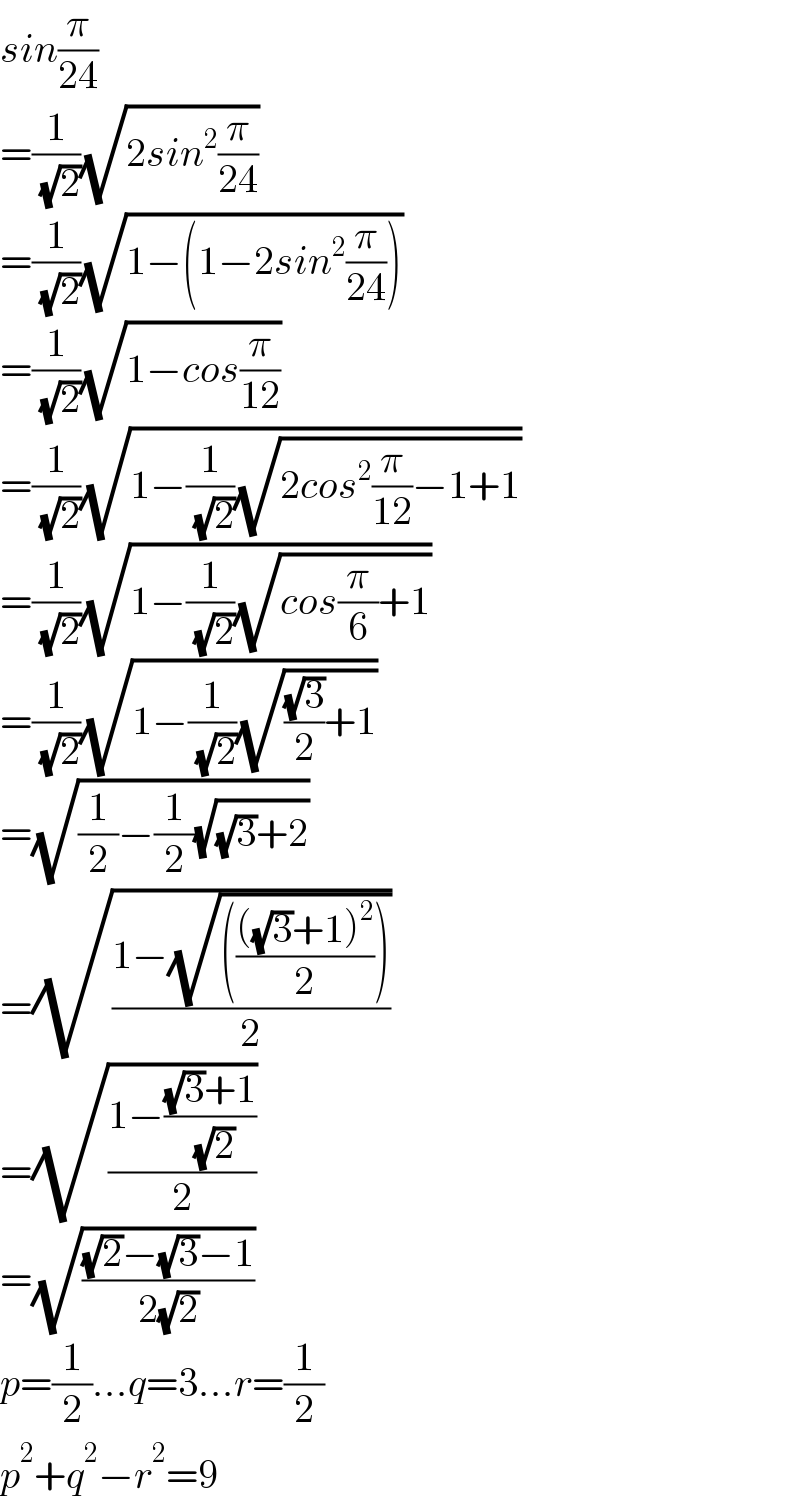
sin(π/(24)) =(1/( (√2)))(√(2sin^2 (π/(24)))) =(1/( (√2)))(√(1−(1−2sin^2 (π/(24))))) =(1/( (√2)))(√(1−cos(π/(12)))) =(1/( (√2)))(√(1−(1/( (√2)))(√(2cos^2 (π/(12))−1+1)))) =(1/( (√2)))(√(1−(1/( (√2)))(√(cos(π/6)+1)))) =(1/( (√2)))(√(1−(1/( (√2)))(√(((√3)/2)+1)))) =(√((1/2)−(1/2)(√((√3)+2)))) =(√((1−(√((((((√3)+1)^2 )/2)))))/2)) =(√((1−(((√3)+1)/( (√2))))/2)) =(√(((√2)−(√3)−1)/(2(√2)))) p=(1/2)...q=3...r=(1/2) p^2 +q^2 −r^2 =9
$${sin}\frac{\pi}{\mathrm{24}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\sqrt{\mathrm{2}{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{24}}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\sqrt{\mathrm{1}−\left(\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{24}}\right)} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\sqrt{\mathrm{1}−{cos}\frac{\pi}{\mathrm{12}}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\sqrt{\mathrm{2}{cos}^{\mathrm{2}} \frac{\pi}{\mathrm{12}}−\mathrm{1}+\mathrm{1}}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\sqrt{{cos}\frac{\pi}{\mathrm{6}}+\mathrm{1}}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\sqrt{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\mathrm{1}}} \\ $$$$=\sqrt{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\sqrt{\mathrm{3}}+\mathrm{2}}} \\ $$$$=\sqrt{\frac{\mathrm{1}−\sqrt{\left(\frac{\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}\right)}}{\mathrm{2}}} \\ $$$$=\sqrt{\frac{\mathrm{1}−\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}}}{\mathrm{2}}} \\ $$$$=\sqrt{\frac{\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}} \\ $$$${p}=\frac{\mathrm{1}}{\mathrm{2}}…{q}=\mathrm{3}…{r}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${p}^{\mathrm{2}} +{q}^{\mathrm{2}} −{r}^{\mathrm{2}} =\mathrm{9} \\ $$
Answered by Dwaipayan Shikari last updated on 19/Feb/21
sin(((23π)/(24)))=sin((π/(24))) 1+cos(π/6)=2cos^2 (π/(12)) ⇒(1/2)(√(2+(√3)))=cos(π/(12)) ⇒1−(1/2)(√(2+(√3)))=2sin^2 (π/(24)) ⇒sin(π/(24))=(1/2)(√(2−(√(2+(√3)))))=(1/2)(√((2(√2)−(√3)−1)/( (√2)))) =(√((2(√2)−(√3)−1)/(4(√2)))) p^2 +q^2 −r^2 =9 As((√(2+(√3)))=(√(3/2))+(√(1/2)))
$${sin}\left(\frac{\mathrm{23}\pi}{\mathrm{24}}\right)={sin}\left(\frac{\pi}{\mathrm{24}}\right) \\ $$$$\mathrm{1}+{cos}\frac{\pi}{\mathrm{6}}=\mathrm{2}{cos}^{\mathrm{2}} \frac{\pi}{\mathrm{12}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}={cos}\frac{\pi}{\mathrm{12}} \\ $$$$\Rightarrow\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}=\mathrm{2}{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{24}} \\ $$$$\Rightarrow{sin}\frac{\pi}{\mathrm{24}}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}−\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\mathrm{2}\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}−\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \\ $$$$=\sqrt{\frac{\mathrm{2}\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}}\:\:\:\:\:\:\:\:\:{p}^{\mathrm{2}} +{q}^{\mathrm{2}} −{r}^{\mathrm{2}} =\mathrm{9} \\ $$$$\:\:{As}\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}=\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}+\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *