Question Number 77347 by key of knowledge last updated on 05/Jan/20
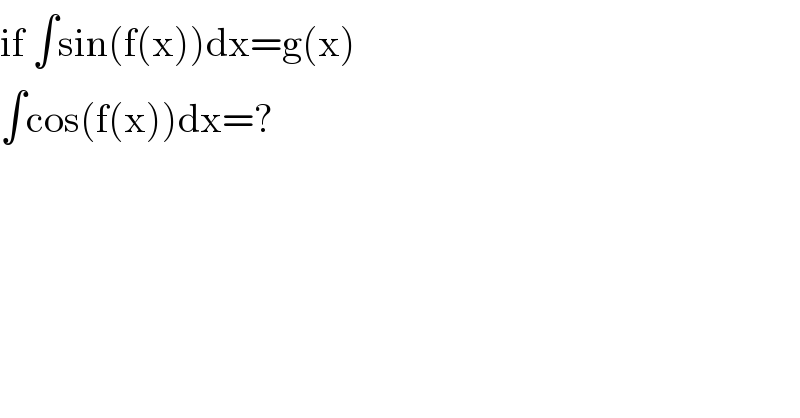
$$\mathrm{if}\:\int\mathrm{sin}\left(\mathrm{f}\left(\mathrm{x}\right)\right)\mathrm{dx}=\mathrm{g}\left(\mathrm{x}\right) \\ $$$$\int\mathrm{cos}\left(\mathrm{f}\left(\mathrm{x}\right)\right)\mathrm{dx}=? \\ $$
Commented by mind is power last updated on 05/Jan/20
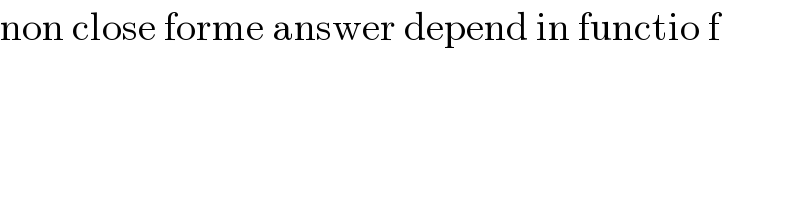
$$\mathrm{non}\:\mathrm{close}\:\mathrm{forme}\:\mathrm{answer}\:\mathrm{depend}\:\mathrm{in}\:\mathrm{functio}\:\mathrm{f}\: \\ $$$$ \\ $$
Answered by Henri Boucatchou last updated on 06/Jan/20
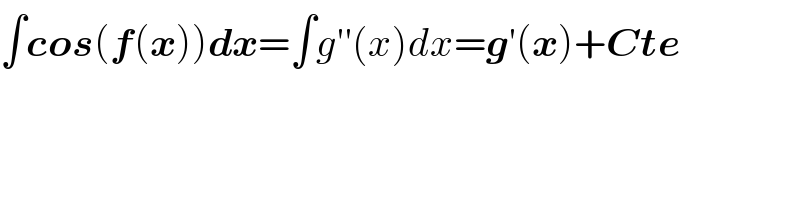
$$\int\boldsymbol{{cos}}\left(\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)\right)\boldsymbol{{dx}}=\int{g}''\left({x}\right){dx}=\boldsymbol{{g}}'\left(\boldsymbol{{x}}\right)+\boldsymbol{{Cte}} \\ $$
Commented by mr W last updated on 06/Jan/20
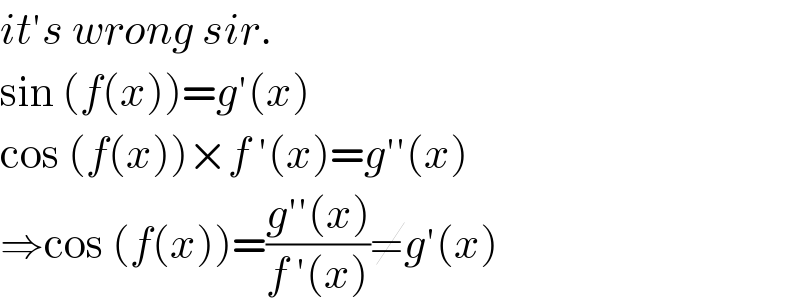
$${it}'{s}\:{wrong}\:{sir}. \\ $$$$\mathrm{sin}\:\left({f}\left({x}\right)\right)={g}'\left({x}\right) \\ $$$$\mathrm{cos}\:\left({f}\left({x}\right)\right)×{f}\:'\left({x}\right)={g}''\left({x}\right) \\ $$$$\Rightarrow\mathrm{cos}\:\left({f}\left({x}\right)\right)=\frac{{g}''\left({x}\right)}{{f}\:'\left({x}\right)}\neq{g}'\left({x}\right) \\ $$
Answered by john santu last updated on 06/Jan/20
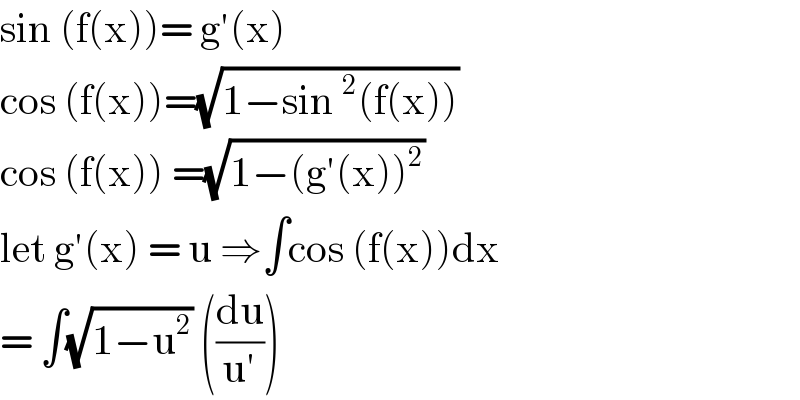
$$\mathrm{sin}\:\left(\mathrm{f}\left(\mathrm{x}\right)\right)=\:\mathrm{g}'\left(\mathrm{x}\right)\: \\ $$$$\mathrm{cos}\:\left(\mathrm{f}\left(\mathrm{x}\right)\right)=\sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{f}\left(\mathrm{x}\right)\right)} \\ $$$$\mathrm{cos}\:\left(\mathrm{f}\left(\mathrm{x}\right)\right)\:=\sqrt{\mathrm{1}−\left(\mathrm{g}'\left(\mathrm{x}\right)\right)^{\mathrm{2}} } \\ $$$$\mathrm{let}\:\mathrm{g}'\left(\mathrm{x}\right)\:=\:\mathrm{u}\:\Rightarrow\int\mathrm{cos}\:\left(\mathrm{f}\left(\mathrm{x}\right)\right)\mathrm{dx} \\ $$$$=\:\int\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }\:\left(\frac{\mathrm{du}}{\mathrm{u}'}\right) \\ $$
