Question Number 143350 by gsk2684 last updated on 13/Jun/21
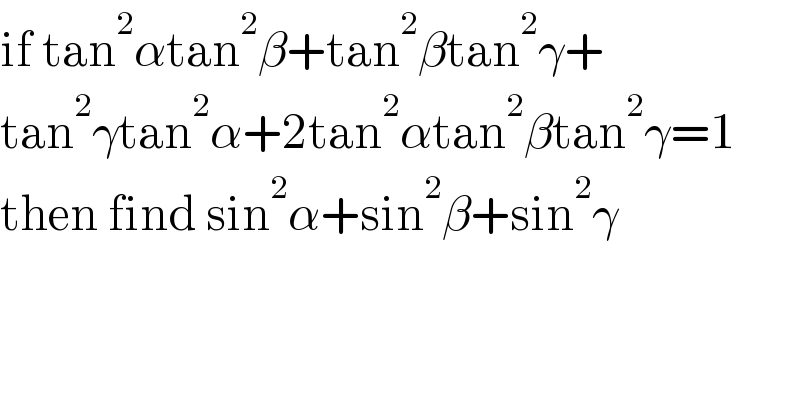
$$\mathrm{if}\:\mathrm{tan}^{\mathrm{2}} \alpha\mathrm{tan}^{\mathrm{2}} \beta+\mathrm{tan}^{\mathrm{2}} \beta\mathrm{tan}^{\mathrm{2}} \gamma+ \\ $$$$\mathrm{tan}^{\mathrm{2}} \gamma\mathrm{tan}^{\mathrm{2}} \alpha+\mathrm{2tan}^{\mathrm{2}} \alpha\mathrm{tan}^{\mathrm{2}} \beta\mathrm{tan}^{\mathrm{2}} \gamma=\mathrm{1} \\ $$$$\mathrm{then}\:\mathrm{find}\:\mathrm{sin}^{\mathrm{2}} \alpha+\mathrm{sin}^{\mathrm{2}} \beta+\mathrm{sin}^{\mathrm{2}} \gamma \\ $$
Answered by mnjuly1970 last updated on 13/Jun/21
![Ω:=sin^2 α+sin^2 β+sin^2 γ :=((tan^2 α)/(1+tan^2 α))+((tan^2 β)/(1+tan^2 β))+((tan^2 γ)/(1+tan^2 γ)) :=((tan^2 α+tan^2 β+tan^2 γ+2tan^2 αtan^2 β+2tan^2 αtan^2 γ+2tan^2 βtan^2 γ+3tan^2 αtan^2 βtan^2 γ)/(1+tan^2 α+tan^2 β+tan^2 γ+tan^2 αtan^2 β+tan^2 βtan^2 γ+tan^2 αtan^2 γ+tan^2 αtan^2 βtan^2 γ)) :=(([tan^2 α+tan^2 β+tan^2 γ+tan^2 αtan^2 β+tan^2 αtan^2 γ+tan^2 βtan^2 γ+tan^2 +tan^2 αtan^2 β+tan^2 γ+1]:=A)/A) =1 ........ Ω:=1 ........ { Note:= sin^2 (x)=((tan^2 (x))/(1+tan^2 (x))) }](https://www.tinkutara.com/question/Q143357.png)
$$\:\:\:\:\:\Omega:={sin}^{\mathrm{2}} \alpha+{sin}^{\mathrm{2}} \beta+{sin}^{\mathrm{2}} \gamma \\ $$$$\:\:\:\:\:\:\:\::=\frac{{tan}^{\mathrm{2}} \alpha}{\mathrm{1}+{tan}^{\mathrm{2}} \alpha}+\frac{{tan}^{\mathrm{2}} \beta}{\mathrm{1}+{tan}^{\mathrm{2}} \beta}+\frac{{tan}^{\mathrm{2}} \gamma}{\mathrm{1}+{tan}^{\mathrm{2}} \gamma} \\ $$$$\:\:\:\:\::=\frac{{tan}^{\mathrm{2}} \alpha+{tan}^{\mathrm{2}} \beta+{tan}^{\mathrm{2}} \gamma+\mathrm{2}{tan}^{\mathrm{2}} \alpha{tan}^{\mathrm{2}} \beta+\mathrm{2}{tan}^{\mathrm{2}} \alpha{tan}^{\mathrm{2}} \gamma+\mathrm{2}{tan}^{\mathrm{2}} \beta{tan}^{\mathrm{2}} \gamma+\mathrm{3}{tan}^{\mathrm{2}} \alpha{tan}^{\mathrm{2}} \beta{tan}^{\mathrm{2}} \gamma}{\mathrm{1}+{tan}^{\mathrm{2}} \alpha+{tan}^{\mathrm{2}} \beta+{tan}^{\mathrm{2}} \gamma+{tan}^{\mathrm{2}} \alpha{tan}^{\mathrm{2}} \beta+{tan}^{\mathrm{2}} \beta{tan}^{\mathrm{2}} \gamma+{tan}^{\mathrm{2}} \alpha{tan}^{\mathrm{2}} \gamma+{tan}^{\mathrm{2}} \alpha{tan}^{\mathrm{2}} \beta{tan}^{\mathrm{2}} \gamma} \\ $$$$\:\:\:\:\:\::=\frac{\left[{tan}^{\mathrm{2}} \alpha+{tan}^{\mathrm{2}} \beta+{tan}^{\mathrm{2}} \gamma+{tan}^{\mathrm{2}} \alpha{tan}^{\mathrm{2}} \beta+{tan}^{\mathrm{2}} \alpha{tan}^{\mathrm{2}} \gamma+{tan}^{\mathrm{2}} \beta{tan}^{\mathrm{2}} \gamma+{tan}^{\mathrm{2}} +{tan}^{\mathrm{2}} \alpha{tan}^{\mathrm{2}} \beta+{tan}^{\mathrm{2}} \gamma+\mathrm{1}\right]:=\mathrm{A}}{\mathrm{A}}\:=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:……..\:\Omega:=\mathrm{1}\:…….. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\left\{\:{Note}:=\:{sin}^{\mathrm{2}} \left({x}\right)=\frac{{tan}^{\mathrm{2}} \left({x}\right)}{\mathrm{1}+{tan}^{\mathrm{2}} \left({x}\right)}\:\right\} \\ $$
Commented by gsk2684 last updated on 13/Jun/21

$$\mathrm{thank}\:\mathrm{you}\: \\ $$
Commented by mnjuly1970 last updated on 13/Jun/21
$$\:\:\:{thank}\:{you}\:{so}\:{much}\:{sir}… \\ $$
